250x250
Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
Tags
- 운영체제
- heapq
- JPA
- python
- 자료구조
- 연결리스트 종류
- 최대 힙
- SpringSecurity
- 점근적 표기법
- 이분탐색이란
- 스케줄링
- 힙트리
- 백준장학금
- HTTP
- MSA
- 알고리즘
- Kruskal
- spring
- jpa n+1 문제
- 완전이진트리
- JVM
- AVL트리
- 엔티티 그래프
- 연결리스트
- posix
- 멀티프로세서
- 프로세스
- 최소힙
- 백준 장학금
- 강화학습
Archives
- Today
- Total
KKanging
[자료구조] 힙트리의 정의 와 구현 (Java) 본문

힙이란
- 완전이진 트리로 구성되었다.
- 트리의 구성이 균형을 이룬다
- 부모노드와 자식 노드 관계에 특징을 이룬다.
힙의 종류
- 최대 힙 트리 (Max heap)
- 완전이진트리로 구성
- 부모 노드의 키 값은 자식 노드의 키 값보다 크거나 같음
- 왼쪽 오른쪽 자식의 크기 구분 없음
- 최소 힙 트리(Min heap)
- 완전 이진트리로 구성된 트리
- 부모 노드의 키 값은 자식 노드의 키 값보다 작거나 같음
- 왼쪽 오른쪽 자식의 크기 구분 없음
힙의 응용
- 우선 순위 큐, 프린터 스풀러 등등
- 힙 정렬: 최대 힙 (내림 차순 정렬) , 최소 힙 ( 오름차순 정렬)
최대 힙 구조
이 글에서는 최대 힙의 예시와 구현만 하였습니다.
최대 힙의 예

배열 표

삽입 연산
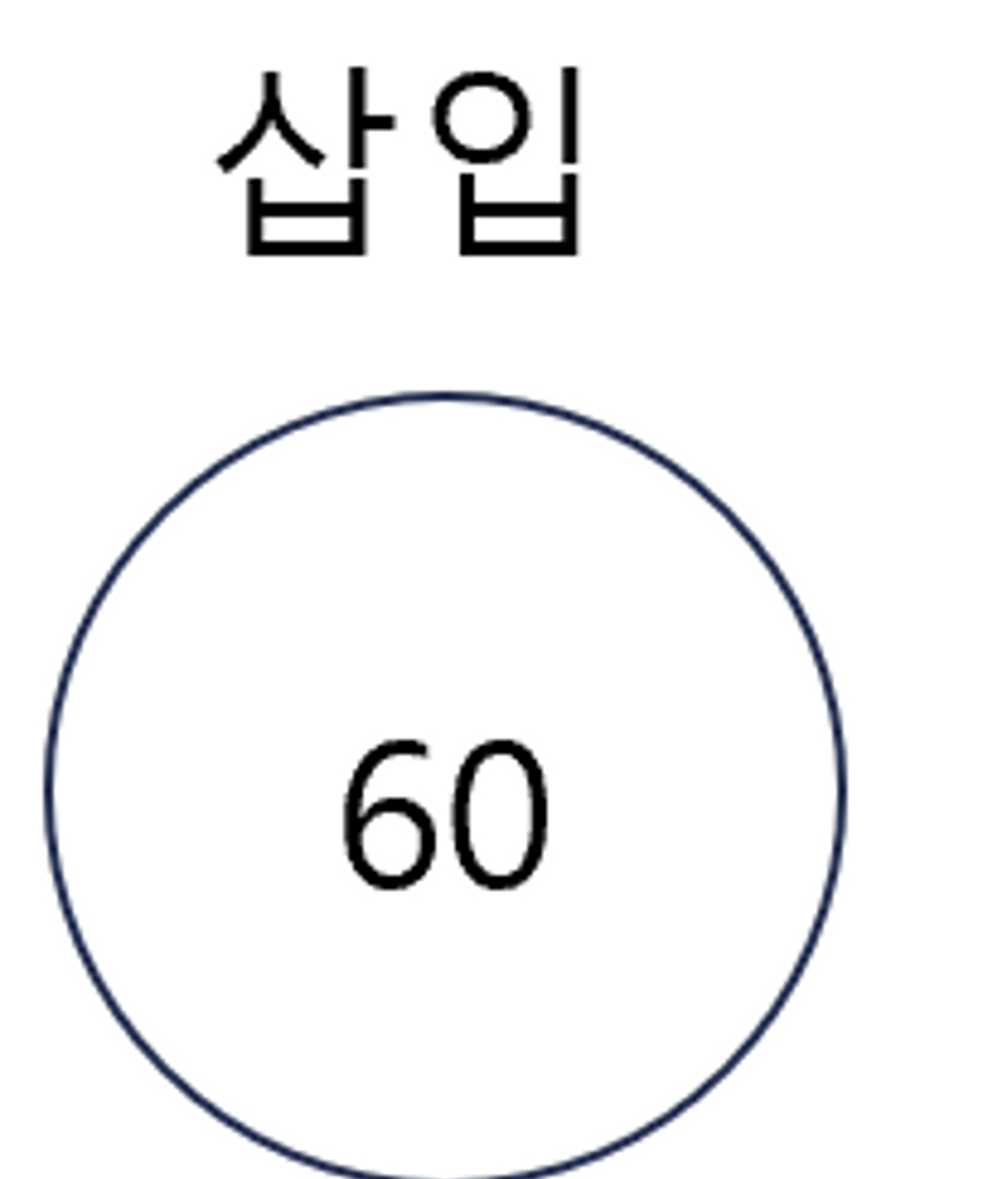
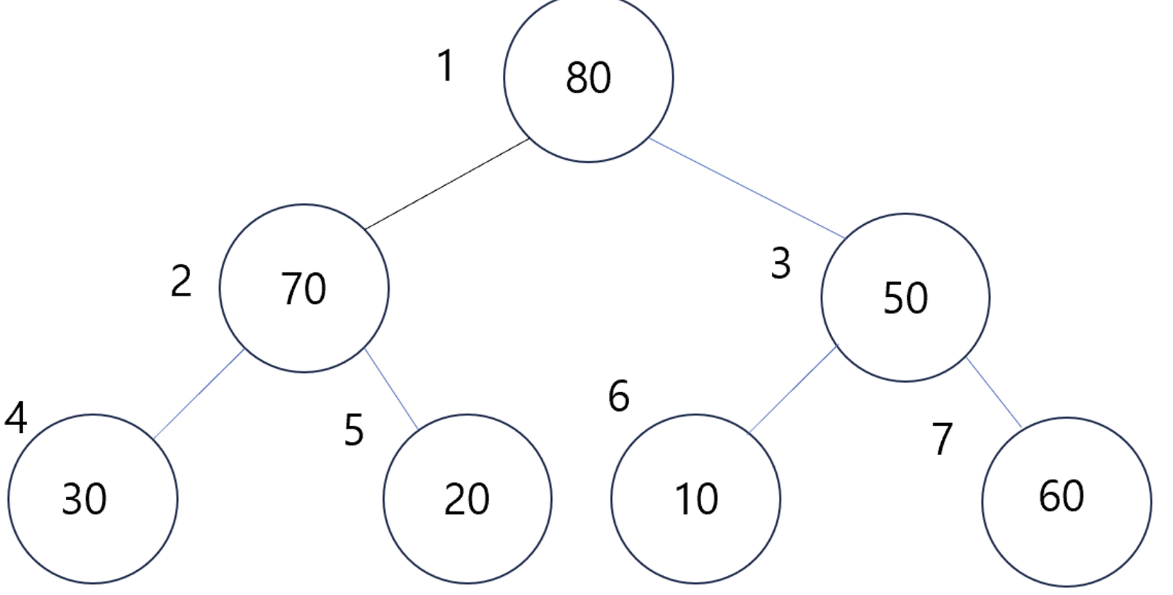
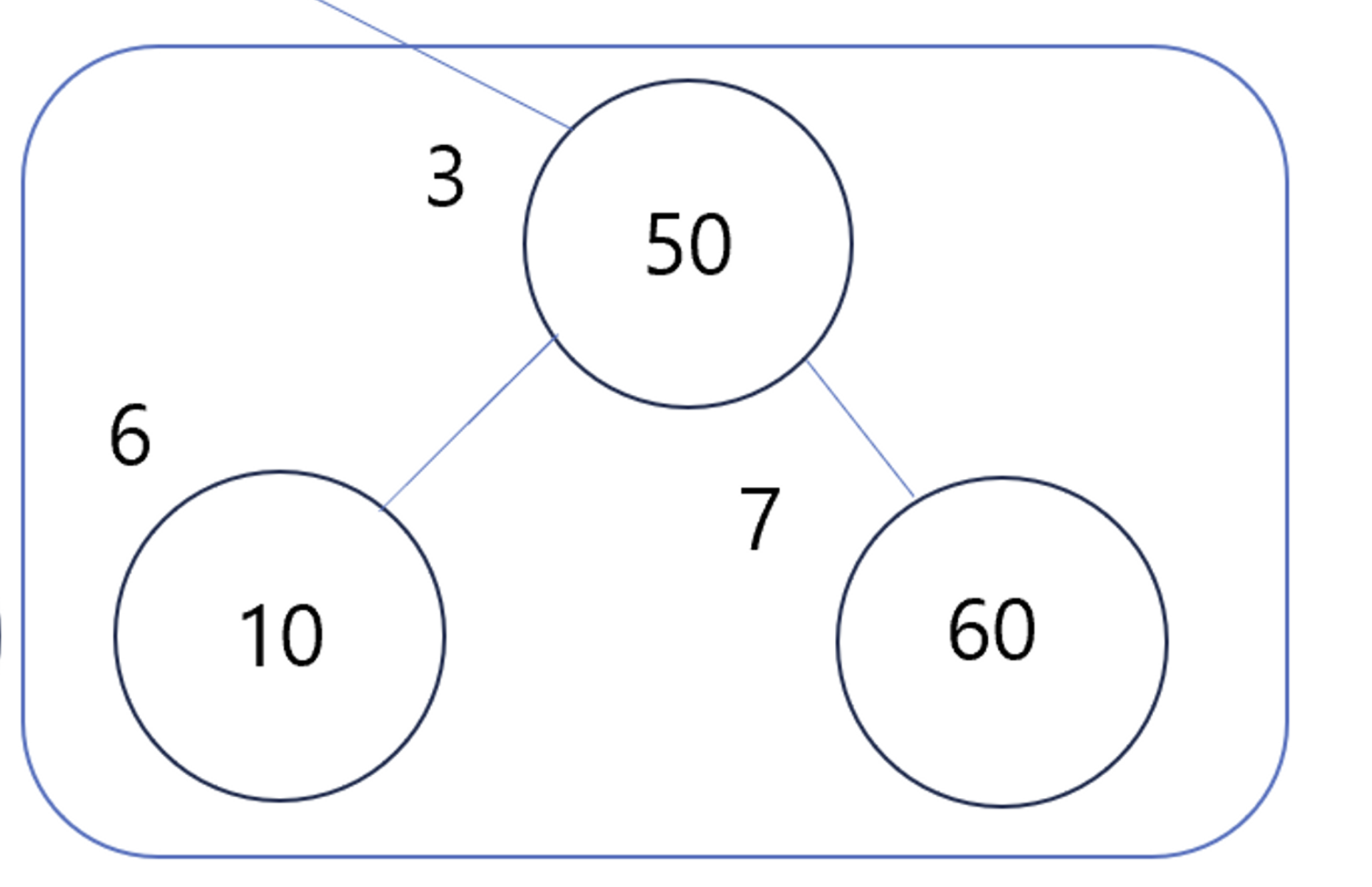
- 그리고 heapify 연산을 한다
- heapify 연산이란 ? 위 그림과 같이 힙 성질에 적합하지 않을 때 위치를 재조정해주는 연산을 말한다.
- 배열로 나타내면 다음과 같다


힙트리를 처음 공부하는 사람은 삽입 삭제 연산이 비효율적이라고 생각할 수 있다.
하지만 힙트리는 위 같은 연산과정을 거치면서 균형을 맞출 수 있게 된다.
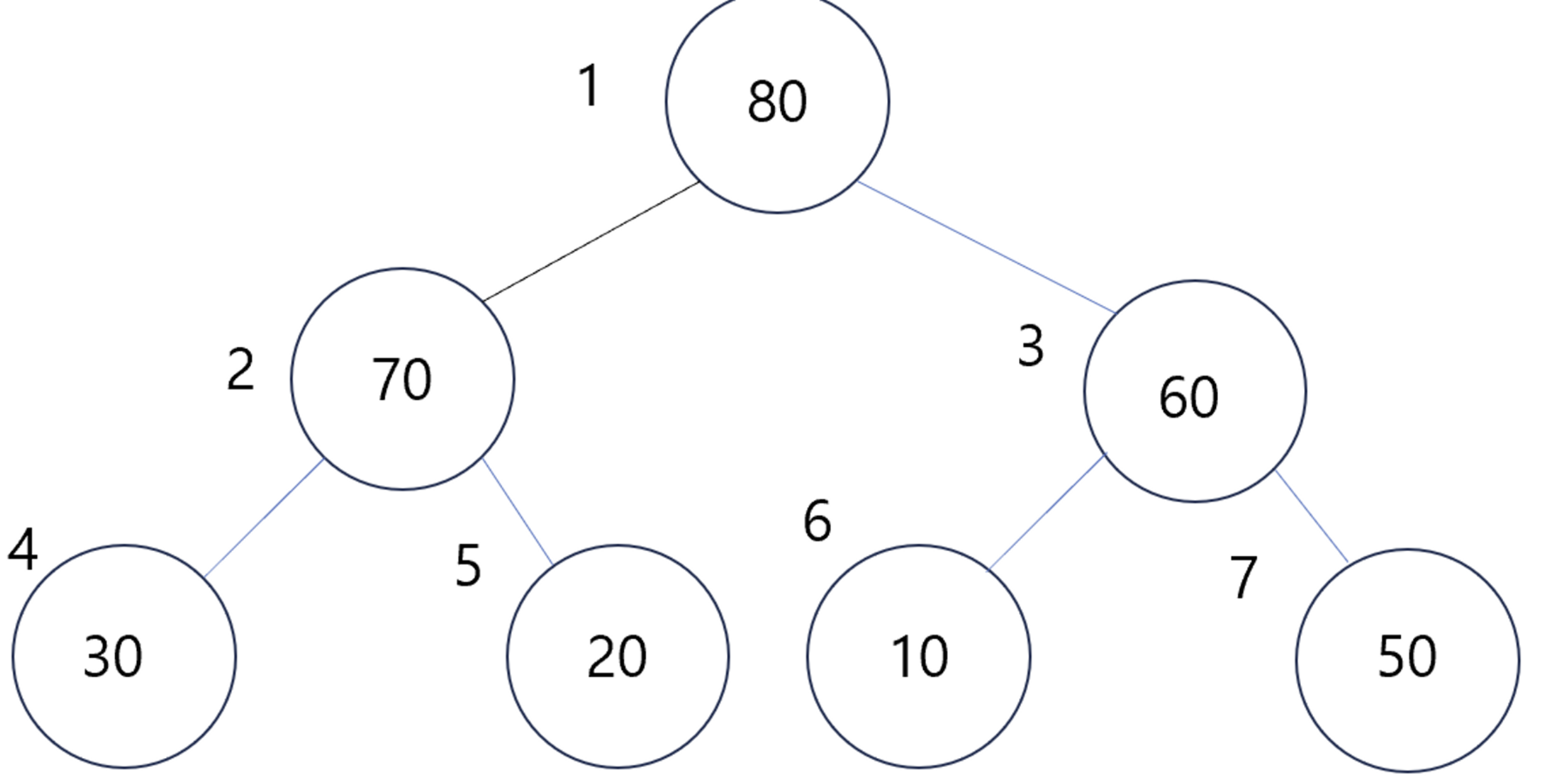
최대 힙 트리의 삭제 연산
- 최대 힙 트리의 삭제 연산은 일반적으로 제일 부모 노드의 삭제만 다룬다.
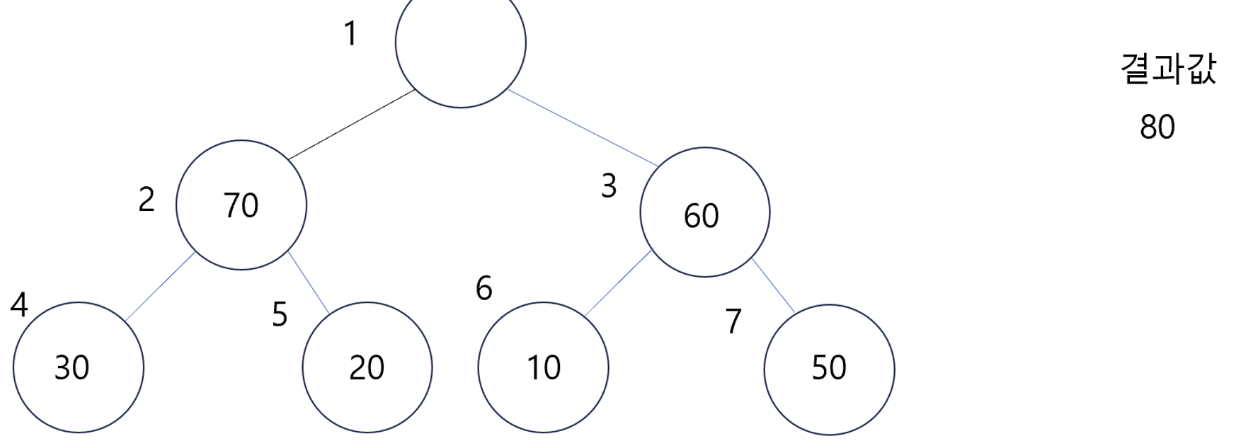
- 위 그림과 같이 최대 힙 트리는 제일 부모노드 즉 삭제 연산 시 트리에서 제일 큰 값을 반환한다.
- 하지만 여기서 연산을 그만 둔다면 힙트리의 균형이 깨질 것이다.
- heapify 연산을 통해 위치를 재조정할 필요가 있다.
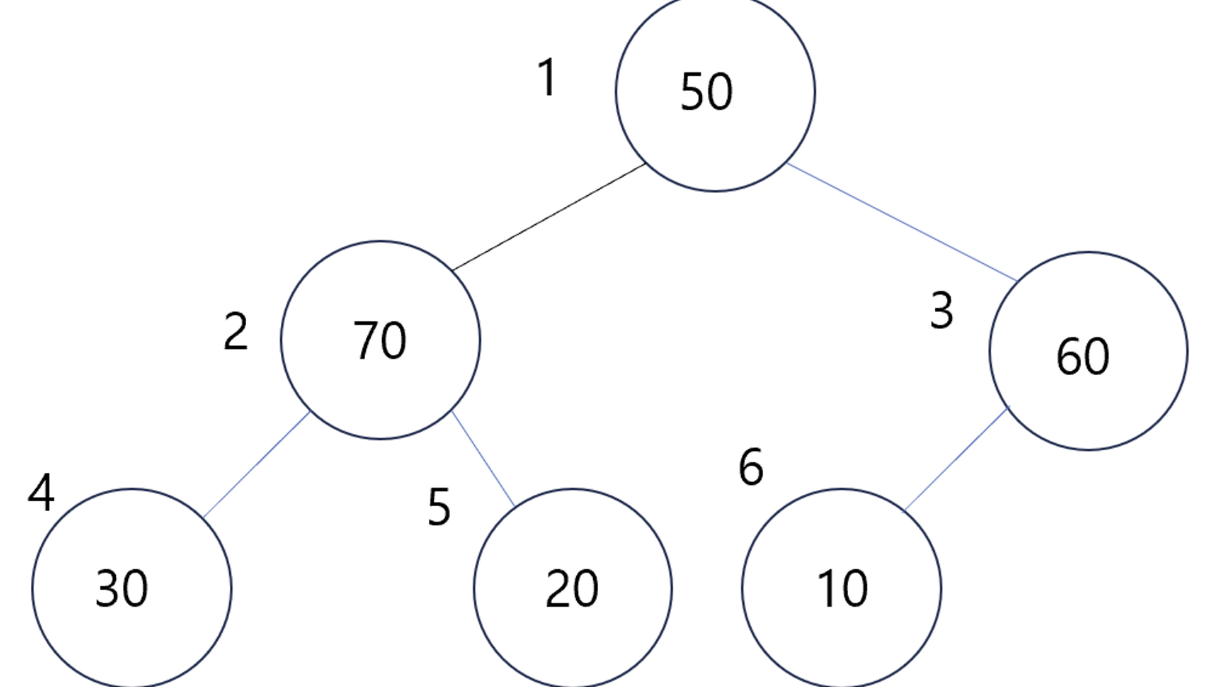
- 우선 삭제된 자리에 제일 마지막 인덱스의 노드를 가지고 온다
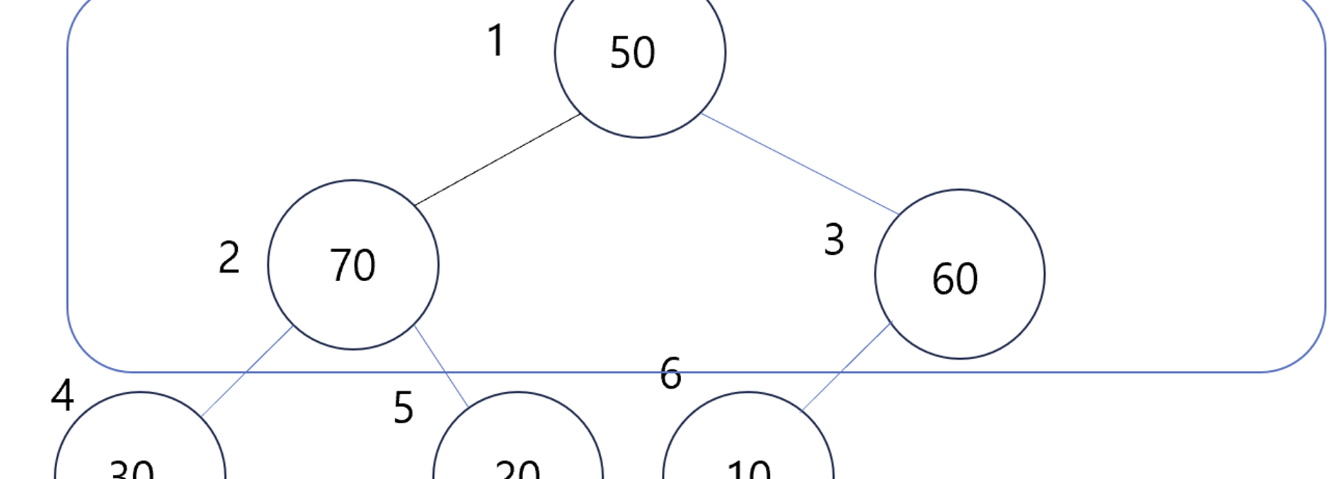
- 그리고 다음과 같이 자식 노드와 비교 후 위치를 바꾸는데,
- 무조건 자식 노드 2개중 더 큰 노드와 비교해야 한다.
- 안 그러면 위치를 바꾼다 하더라도 균형이 깨질 것이다.
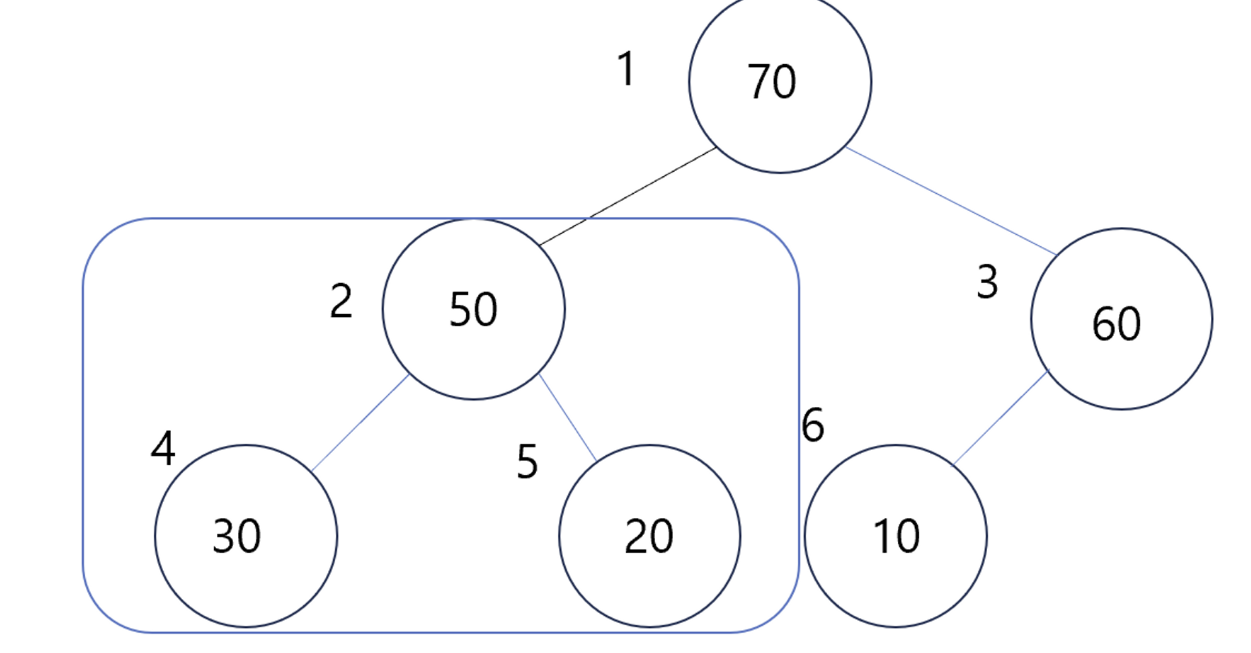
- 다음과 같이 트리 중 제일 큰 값이 조상 노드로 갔다.
- 그다음은 heap트리를 만족하므로 연산을 break 한다.
배열로 나타내면 다음과 같다.
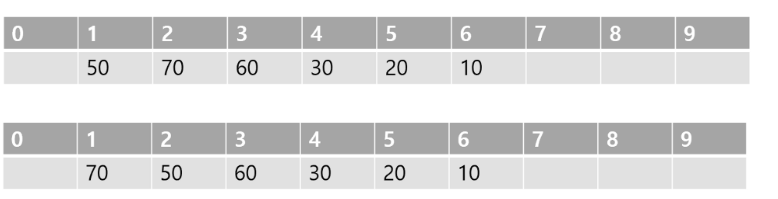
힙트리의 수행시간
- 삽입: O(logn)
- 삭제: O(logn)
heap 트리의 응용
힙트리는 수행시간이 효율적인 만큼 알고리즘 문제에서 우선순위 큐나 heap 정렬에서 자주 쓰입니다.
우선순위 큐
- 우선순위 큐
- → 우선순위 큐란 가장 우선순위가 높은 데이터를 먼저 꺼내는 구조의 데이터 구조이다.
- heap트리를 이용하여 구현
heap 정렬
- 반대로 Min-heap 정렬 같은 경우는 오름차순 정렬이 될 것이다.
- 수행시간: O(nlogn) 아주 효율적인 알고리즘이다.
- 위에와 같이 삭제 연산을 계속 수행하면 Max-heap 같은 경우 내림 차순 정렬이 될 것이다.
JAVA 구현
package Main;
public class Max_heap {
private int []arr;
private int size;
private int index;
public Max_heap(){
this(10);
}
public Max_heap(int size){
this.size = size;
arr = new int[this.size];
arr[0] = 0; // 0인덱스를 일부로 비움
this.index = 1;
}
public void Insert(int data){
if (this.index==1){
arr[index] = data;
index++;
return;
}
if (this.index == this.size){
return; // 용량 초과
}
else{
int child;
int parrent;
arr[index] = data;
child = index;
index++;
parrent = (int)child/2;
while (parrent > 0){
if (arr[parrent] < arr[child]){
int temp = arr[parrent];
arr[parrent] = arr[child];
arr[child] = temp;
child = parrent;
parrent = (int)child/2;
}
else{
break;
}
}
}
}
public int Delete(){
if (this.index == 1){
return -1;
}
int result = arr[1];
this.index--;
arr[1] = arr[this.index];
int parrent = 1;
int child = parrent*2;
while (child < this.index){
if (child + 1 < this.index && arr[child] < arr[child+1]){
child ++;
}
if (arr[parrent] < arr[child]){
int temp = arr[parrent];
arr[parrent] = arr[child];
arr[child] = temp;
parrent = child;
child = parrent*2;
}
else{
break;
}
}
return result;
}
public void Print() {
if (this.index == 1){
System.out.println("값없음");
return;
}
for (int i = 1; i < this.index; i++) {
System.out.print(arr[i] + "->");
}
System.out.println();
}
}'cs > 자료구조' 카테고리의 다른 글
| [자료구조] 이진탐색트리의 개념과 구현(Java) (0) | 2023.07.24 |
|---|---|
| [자료구조] 이진트리란 && 전위 중위 후위 순회 구현(Java) (0) | 2023.07.20 |
| [자료구조] 완전 이진트리란? (0) | 2023.07.14 |
| [자료구조] 트리란? (0) | 2023.07.13 |
| [자료구조] 덱(Deque)의 개념과 구현(Java) (0) | 2023.07.11 |





