250x250
Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
Tags
- 알고리즘
- AVL트리
- 프로세스
- 스케줄링
- SpringSecurity
- 멀티프로세서
- JPA
- 연결리스트 종류
- JVM
- 최대 힙
- 최소힙
- 백준장학금
- Kruskal
- spring
- python
- 완전이진트리
- jpa n+1 문제
- 이분탐색이란
- MSA
- 백준 장학금
- 운영체제
- 자료구조
- posix
- 엔티티 그래프
- HTTP
- 점근적 표기법
- 강화학습
- 연결리스트
- heapq
- 힙트리
Archives
- Today
- Total
KKanging
[자료구조] AVL 트리란 본문
*** AVL트리는 이진탐색트리의 종류입니다. 이진탐색트리의 개념을 모른다면 보는 것을 추천합니다
https://kkangmg.tistory.com/15
1. AVL 트리
이진 탐색 트리의 단점
- 이진 탐색 트리는 평균 복잡도가 O(logn)으로 효율적인 트리이다.
- 하지만 트리의 균형(balance)이 깨지면 O(n)으로 비효율적인 트리가 된다.
- 비효율적인 이진 탐색 트리
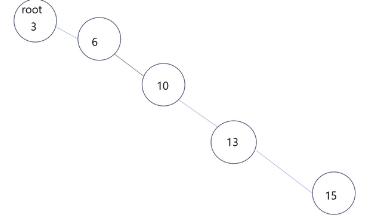
AVL 트리란
- 발명자인 Adelson-Velsky and Landis 에서 따온 이름
- 이진 탐색 트리의 종류
- 자가 균형 이진 탐색 트리이다.
- 이진탐색트리의 단점을 보완하여 트리의 균형을 유지한다.
- 검색, 삽입 , 삭제 연산에서 평균과 최악 둘 다 O(logn)의 시간 복잡도를 가진다.
원리
- 트리의 높이를 통해 균형도(Balance Factor)를 검사하고
- 트리의 좌우 높이(h)의 균형(balance)이 깨질 때마다 균형을 잡는 연산을 통해 균형을 잡는다.
- 연산은 회전(rotation)을 통해 이루어 진다.
균형도(Balance Factor)란?
- 균형도란 (왼쪽 서브트리의 높이 - 오른쪽 서브 트리의 높이)이다.
- 아래 그림에서 각 노드 별 높이와 균형도를 나타냈다.
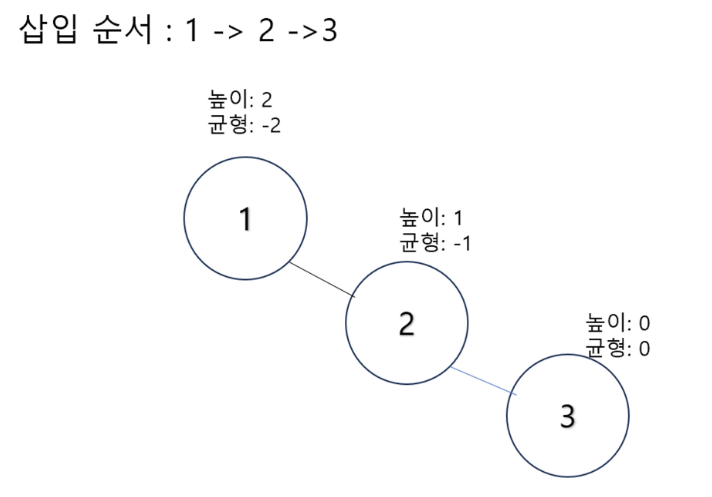
AVL 트리의 균형도
- AVL 트리의 균형도는 -1, 0 , +1 만 가진다는 성질이 있다.
- -1,0,1을 제외한 숫자의 균형도를 가지면 균형을 맞추는 연산을 한다(회전).
- 위 그림과 같이 3을 마지막으로 삽입했을 때 리프 노드부터 위로 올라가면서(무조건 아래에서부터 위로 검사해야 한다.) 균형도를 검사하고 균형도가 깨지면 회전을 한다.
- 참고, 높이와 균형도는 아래서부터 계산한다.
- 높이와 균형도 식

회전이란(Rotation)
- AVL 트리에서 회전은 부모 노드와 그 자식 노드들 간의 구조를 변경하는 트리 조작 작업
- 회전은 4가지 문제에서 연산한다.
- RR(right-right) 문제
- LL(left-left) 문제
- RL(right-left) 문제
- LR(left-right) 문제
2. 회전 연산

💡 NULL의 높이와 균형도는 -1이다.
RR문제
- 아래 상황은 1을 기준으로 오른쪽 오른쪽으로 쏠렸다 해서 RR문제이다.

- RR문제는 2의 노드의 왼쪽 자식에 1의 왼쪽 노드를 할당하고
- 2의 왼쪽 자식에 1의 노드를 할당한다.
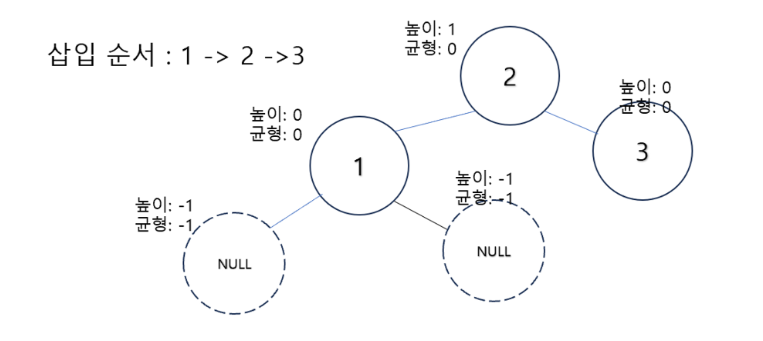
LL문제
- LL 문제는 RR와 비슷하게 왼쪽 왼쪽으로 쏠린 경우다.

- 밑에서부터 균형도를 계산했을 때 1 노드에서 균형도가 깨지는 걸 알 수 있다.
- 2 노드도 깨지지만 아래에서부터 계산하므로 1 노드가 최초로 깨진다.
- RR 문제와 비슷하게 0의 오른쪽 노드를 1의 왼쪽 노드로 0의 오른쪽 노드를 1로 할당하면 된다.
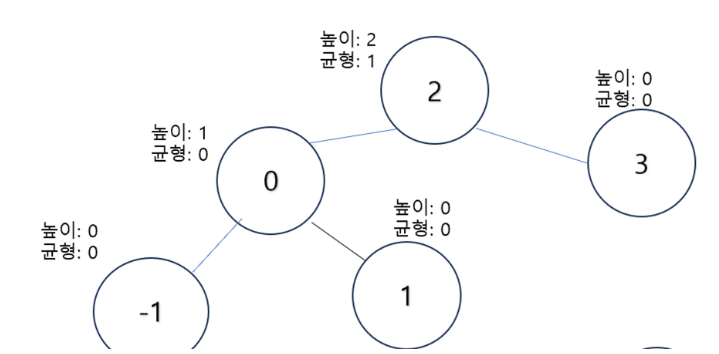
- 주의) 여기서 연산을 멈추면 안 된다.
- 그다음인 2 노드의 균형도까지 계산하고 연산을 그만둬야 한다.
- 만약 또 균형이 깨진다면 회전을 해야 한다.
RL 문제
- RL문제는 RR문제와 LL을 사용하면 된다.
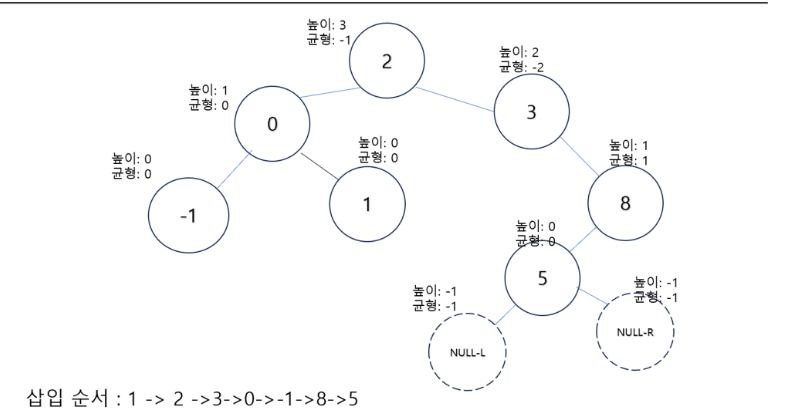

- 최초로 균형도가 깨지는 순간은 3 노드이다.
- 이때 오른쪽 왼쪽으로 쏠리는 걸 볼 수 있다.
- 이 부분을 보면 LL연산을 수행한다.
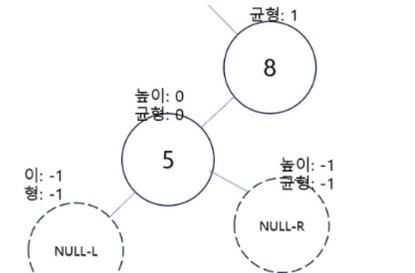
- 이제 RR 연산을 하면 된다.

LR 문제는 RL 문제와 같은 로직이므로 따로 설명을 안 한다.
3. AVL트리의 삽입 삭제 검색
- AVL트리의 삽입 삭제 검색 알고리즘은 기본 이진탐색 트리와 동일하다.
- 하지만 이진탐색트리와 다르게 균형이 깨지지 않으므로 최악의 경우도 평균도 시간 복잡도는 O(logn)으로 효율적이다.
단점
- 균형이 깨지지 않아서 삽입 삭제 검색에는 효율적이나
- 균형을 유지하는 연산에서의 수행시간이 걸린다.
'cs > 자료구조' 카테고리의 다른 글
| [자료구조] 최소 신장 트리(MST: Minimum Spanning Tree)란 (0) | 2023.08.06 |
|---|---|
| [자료구조]그래프란 (0) | 2023.07.27 |
| [자료구조] 이진탐색트리의 개념과 구현(Java) (0) | 2023.07.24 |
| [자료구조] 이진트리란 && 전위 중위 후위 순회 구현(Java) (0) | 2023.07.20 |
| [자료구조] 힙트리의 정의 와 구현 (Java) (0) | 2023.07.15 |





