250x250
Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
Tags
- 이분탐색이란
- 강화학습
- 최대 힙
- posix
- MSA
- 완전이진트리
- 최소힙
- 알고리즘
- 점근적 표기법
- Kruskal
- 자료구조
- 스케줄링
- jpa n+1 문제
- 백준장학금
- 힙트리
- 운영체제
- SpringSecurity
- JVM
- AVL트리
- 엔티티 그래프
- python
- 연결리스트
- 연결리스트 종류
- HTTP
- heapq
- JPA
- 프로세스
- 백준 장학금
- 멀티프로세서
- spring
Archives
- Today
- Total
KKanging
[알고리즘] 이분 탐색이란(Binary Search) 본문
이분 탐색이란
이분 탐색의 특징
- 일반적으로 크기가 N인 배열이 순서대로 정렬되어 있을 때 사용할 수 있다.
- 수행시간이 O(logn)으로 완전 탐색 알고리즘 보다 훨씬 단축된다.
이분탐색은 왜 필요로 할까

- 위와 같은 N=5 배열이 있고 우리는 배열의 원소를 찾는 과정을 수행한다고 가정해보자
- 만약 브루트 포스 알고리즘 ( 완전 탐색 알고리즘)을 사용한다면?
- 1을 찾는다면 한번에 찾을 수 있다.
- 하지만 20을 찾는다면 20을 찾을 때까지 5번의 수행을 해야한다.
- 위 예시는 배열의 크기가 작지만 1024개의 크기라고 가정하면 1024번을 수행한다.
이분탐색의 원리

- 찾는 대상 20
- mid 인덱스 값을 구한다
- 이때 mid 인덱스는 탐색하는 배열의 첫 원소와 마지막 원소의 인덱스의 중간값이다.
- mid = (start+end)/2
- mid 인덱스의 원소와 찾는 대상의 값과 크기를 비교한다.
- 8은 20보다 작은 걸 알 수 있다.
- 센스가 좋다면 8을 포함하고 mid 인덱스 보다 작은 것 중에 찾을 수 없는 걸 알 수 있다.
- 찾는 값이 확실히 없다고 보이는 원소를 배제한다.
- 배제하는 방법은 배열을 삭제하는 것이 아닌 start 원소만 조정해주면 된다.

- 위 1,2,3 의 과정을 찾는 대상을 찾을 때까지 반복하면 된다.
- 위는 (start+end)/2 는 무조건 바닥함수(내림)으로 정의하겠다.
- 그럼 start와 비교하고 start는 작으므로 배제한다.
- 이제 20과 비교하고 20을 찾았으므로 연산을 종료한다.
이분탐색의 효율성
- 위 과정은 크기가 작아서 그렇게 큰 차이를 못 느낄 것이다.
- 만약 크기가 1024개라면?
- 브루트포스 최악의 경우 : 1024번
- 이분탐색 최악의 경우: 10 번
- 위 결과를 보면 얼마나 큰 차이인지 알 수 있을 것이다.
이분 탐색의 활용
- 이분 탐색을 활용하는 방법을 다루겠다.
- 위 예시처럼 정렬된 배열의 수를 빨리 찾는 경우에도 쓰이지만 최적화 문제에도 사용할 수 있다.
이분 탐색을 활용한 최적화 문제
- 어떤 조건을 만족하는 값의 최솟값을 구하는 문제
- 하지만 모든 만족하는 최솟값을 구하는 문제에 적용할 순 없다.
- 밑에 예시를 통해 알아 보겠다.

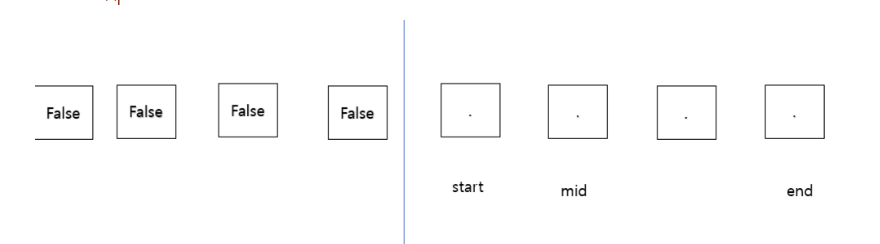
- 위 와같은 배열이 있다고 가정한다.
- 연산 순은 위의 이분탐색과 동일하다.
-
- 불만족하는 경우
- 이 문제가 이분탐색을 적용할 수 있다면 불만족하는 경우 탐색하는 인덱스 기준으로 배제하는 영역을 정할 수 있어야한다.
- 이 문제에서는 mid 값을 검사 했을 때 왼쪽 인덱스 영역을 검사할 필요가 없다고 생각하자mid 인덱스 값과 찾는 조건에 만족하는 지 본다.
- 불만족하는 경우
-
- 만족하는 경우
- 만약 mid 인덱스 원소가 조건을 만족한다고 가정하자
- 그럼 우리는 조건을 만족하는 최솟값을 구하는게 목적이니 mid 인덱스보다 큰 인덱스에 만약 조건을 만족하는 원소가 있다고 해도 mid값보다 큰 값이므로 탐색할 필요가 없어진다.영역을 줄이고 다시 반복한다.
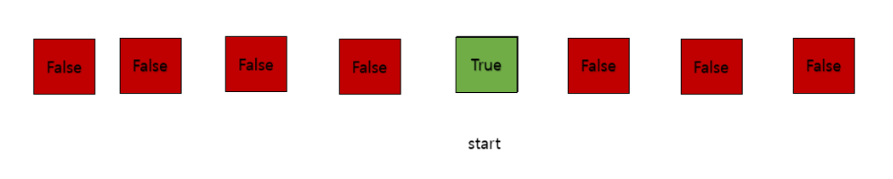
- 만족하는 경우

- 이제 마지막 start 값만 탐색하고 조건을 만족하는 경우면 end 인덱스를 배제할 것이다.(2번 과정 처럼 굳이 start 인덱스가 만족한다면 그것보다 큰 인덱스를 탐색할 필요가 없어서
- 위 예시는 참이라고 가정해보자.
- 이제 하나만 남았으므로 탐색을 종료한다.
정리
- 위 예시를 볼 수 있듯이 이분탐색의 의미는 정렬된 데이터를 중간값 부터 탐색해서 조건을 만족하는지 만족하는 지 검사 후 영역을 배제하는 의미를 가진다.
- 한번 탐색마다 반을 배제하므로 수행시간은 최악이 O(logn)으로 아주 효율적인 알고리즘이다.
- 알고리즘 문제를 많이 풀어보고 다양한 이분탐색 문제를 접해보는 것을 추천한다.
'cs > 알고리즘' 카테고리의 다른 글
| [알고리즘] 버블, 삽입, 퀵 정렬 알고리즘 구현 (java) (0) | 2023.08.20 |
|---|---|
| [알고리즘]Kruskal 알고리즘(java 구현) (0) | 2023.08.20 |
| [알고리즘] 브루트 포스 (완전 탐색)알고리즘이란 (0) | 2023.08.13 |
| [알고리즘] 분할 정복이란 (divide conquer) (0) | 2023.08.07 |
| [알고리즘] greedy 알고리즘 (탐욕 알고리즘) (0) | 2023.08.06 |



