250x250
Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
Tags
- 연결리스트 종류
- 알고리즘
- 운영체제
- Kruskal
- 백준 장학금
- python
- heapq
- 점근적 표기법
- 백준장학금
- 강화학습
- spring
- posix
- 최대 힙
- jpa n+1 문제
- 자료구조
- 멀티프로세서
- HTTP
- AVL트리
- 힙트리
- 연결리스트
- 프로세스
- MSA
- 최소힙
- SpringSecurity
- 스케줄링
- JPA
- 완전이진트리
- 엔티티 그래프
- JVM
- 이분탐색이란
Archives
- Today
- Total
KKanging
[알고리즘]Kruskal 알고리즘(java 구현) 본문
Kruskal 알고리즘
Kruskal 알고리즘이란
→ 가중치 그래프의 자료구조를 이용하여 최소신장트리를 구성하는 알고리즘이다.
→ greedy 알고리즘의 대표적인 알고리즘이다
목차
- 그래프와 최소신장 트리의 개념
- greedy 알고리즘이란
- kruskal 알고리즘
그래프란
→ 노드(정점 vertex)와 그 노드를 연결하는 간선을(edge) 하나로 모아놓은 자료구조
- 무방향 그래프: 간선이 방향이 없는 그래프
- 방향 크래프: 간선의 방향이 있는 그래프

그래프의 표현 방법
- 인접 행렬
- 인접 리스트
인접행렬
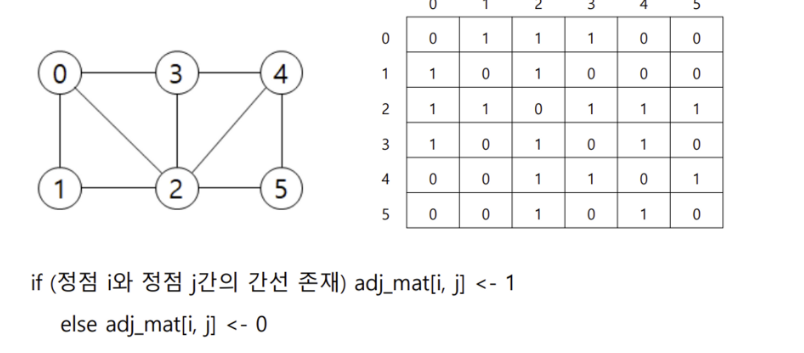
가중치 그래프란
- 그래프의 간선에 가중치(weight)를 부여한 것

트리란
→ 그래프의 한 종류
→ Cycle이 불가능 (그래프에서 사이클(Cycle)이란 어떤 특정 정점에서 출발하여 간선과 정점들을 지 나 다시 처음에 출발했던 특정 정점으로 되돌아오는 것을 말한다.)
→ 부모 - 자식 관계
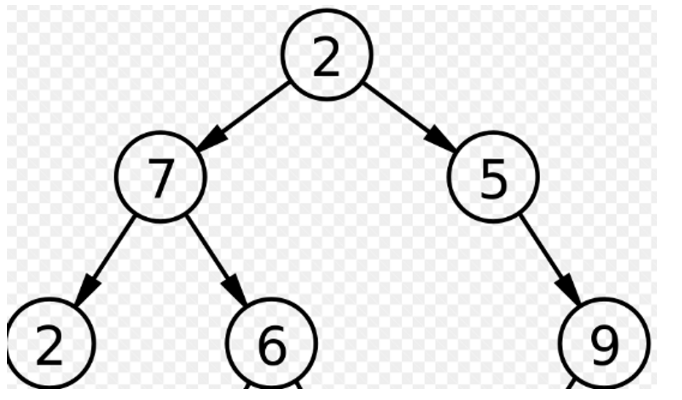
최소신장 트리(MST: Minimum Spanning Tree)란
- 그래프의 정점이 다 포함되어있는 트리( 신장 트리 (spanning tree))
- 가중치 그래프가 주어질 경우 간선들의 비용 합이 최소가 되는 신장 트리
- cycle이 발생하면 안됨
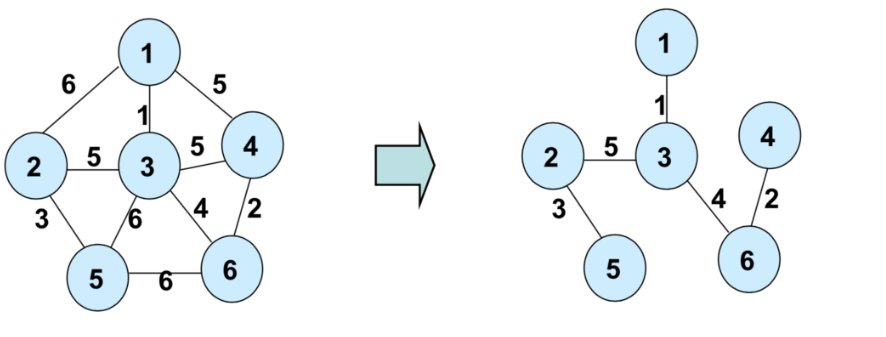
greedy 알고리즘이란
- 매 선택의 순간마다 순간 (local)에 최적인 답을 선택하여 전체 최적해를 구할거라고 기대를 하는 알고리즘이다
- 순간마다의 최적이라고, 그 순간들을 수집한 최종적인 해답이 최적해를 보장하지는 않는다 (하지만 최적해를 보장하는 예는 계산 속도가 엄청 빠르다)
-greedy 알고리즘을 적용하기 좋은 조건
→ greedy 알고리즘은 항상 최적해를 보장하지는 않지만 최적해를 보장하는 2가지 조건이 있다
- 탐욕적 선택 속성: 앞의 최적해 선택이 이후의 최적해 선택에 영향을 주지않는다.즉, 탐욕적 선택으로 전체 문제의 최적해를 반드시 구할 수 있다는 것을 보여야 한다.
- 최적 부분 구조 : 문제에 대한 최종 해결 방법은 부분 문제에 대한 최적 문제 해결 방법으로 구성된다.
-greedy 알고리즘의 문제 해결 방법
- 선택 절차: 현재 local에서 최적해를 선택
- 적절성 검사: 선택된 해가 문제의 조건을 만족하는지 검사
- 해답 검사: 원래의 문제가 해결되었는지 검사하고, 해결되지 않았다면 선택 절차로 돌아가 위의 과정을 반복한다
-대표적인 greedy 알고리즘 문제
- 거스름돈 문제
- 500원 100 50원 10원 1원 (각 동전이 다른 동전의 배수인 경우) 최적해 보장O
- 500원 400원 100원 ( 각 동전이 다른 동전의 배수가 아닌 경우) 최적해 보장X
- 이유는 각 동전이 다른 동전의 배수가 아니면 큰 동전이 작은동전을 표현 못하기때문에 큰 동전을 선택했을 때 최적해를 보장 안할 수가 있다.
-greedy 알고리즘의 장단점
- 장점: 계산 속도가 빠르다(DP와 비교했을때)
- 단점: 최적해를 항상 보장하지 않는다(보장하지 않을때는 다른 알고리즘이나 DP 알고리즘을 사용한다)
-greedy 알고리즘 백준 문제 모음집
문제집: 코딩 테스트 완전 정복 - Greedy(그리디), 탐욕 필수 문제 (park780172)
가중치 그래프로 최소 신장 트리를 구성하는 방법
- Prim 알고리즘
- kruskal 알고리즘
Kruskal알고리즘의 원리
- edge들을 오름차순으로 정렬한다
- 정렬된 edge들을 결합 ( 선택 절차)
- edge들을 결합할때마다 (적절성 검사)
- 해답 검사 조건을 만족하지 않으면 2번으로 반복
Kruskal 알고리즘
- edge들을 오름차순으로 정렬한다
- 정렬한알고리즘 순서대로 트리를 구성한다
하지만 그냥 무작정 구성하다보면 cycle이 발생한다
그러면 cycle이 발생하면 무시하는 방법을 사용
- 그래서 각 정점을 포함하는 하나의 트리가 만들어질때까지 구해나간다
- 이 예에는 없지만 중간에 cycle이 발생하면 연결을 무시
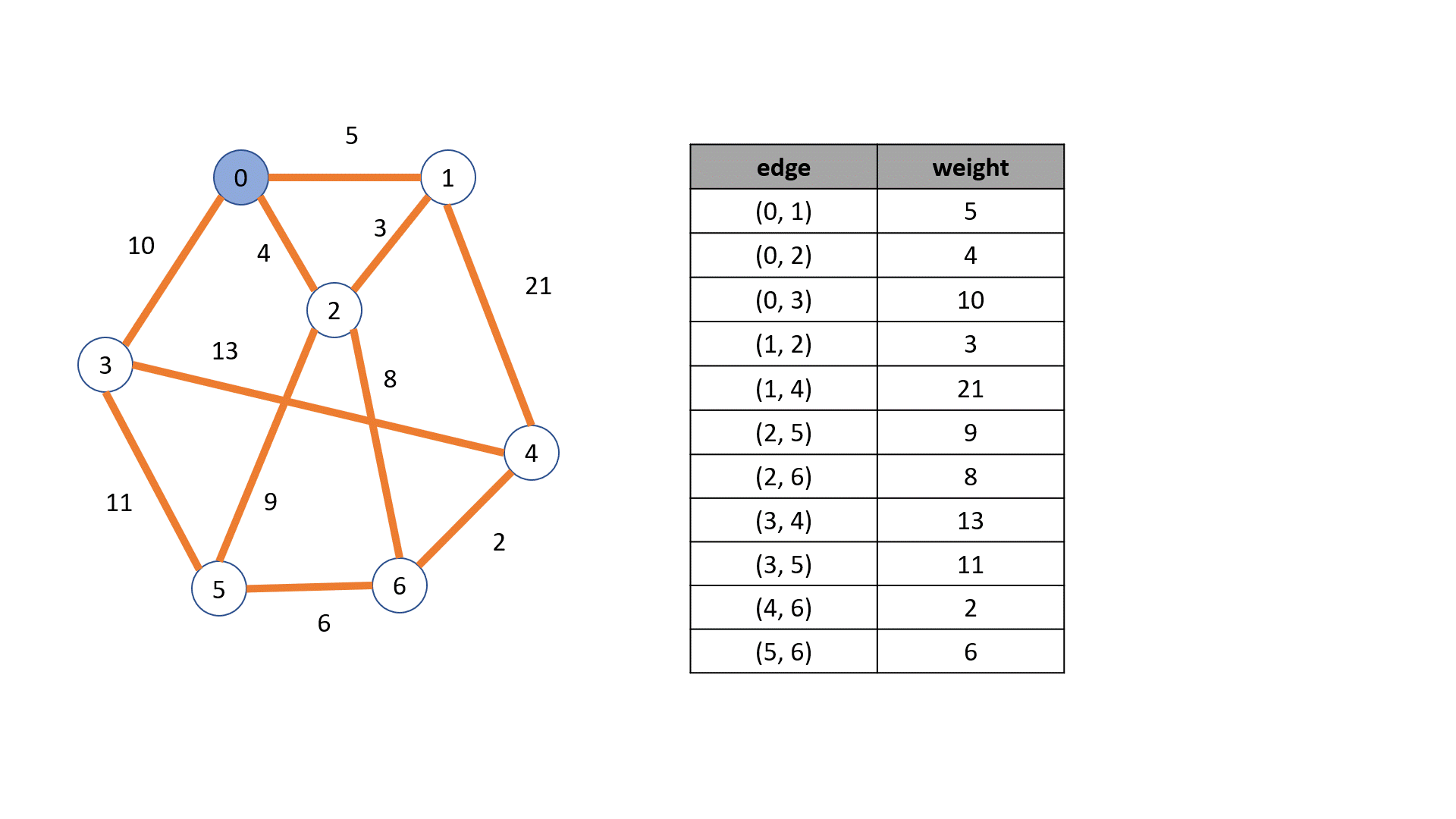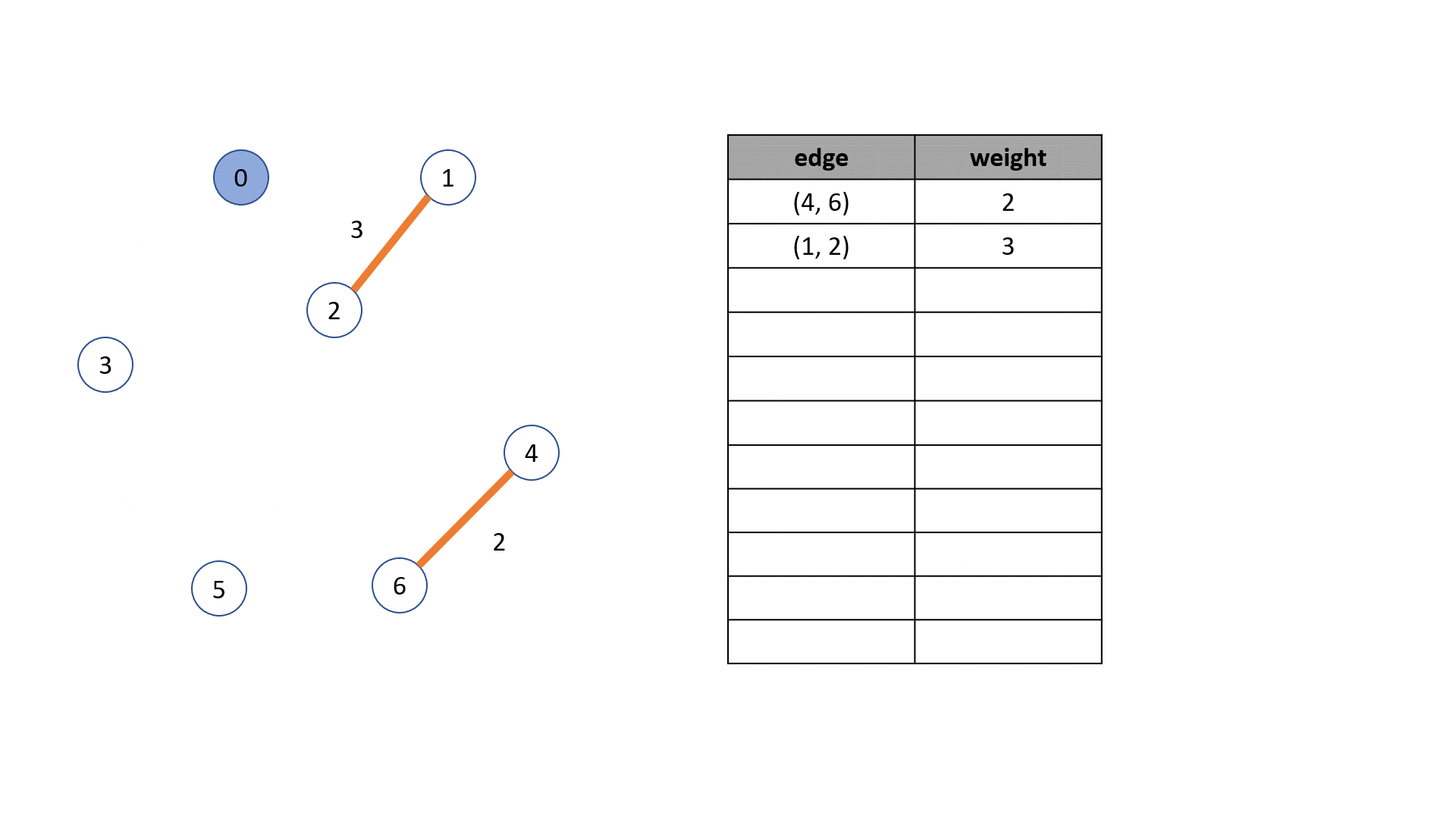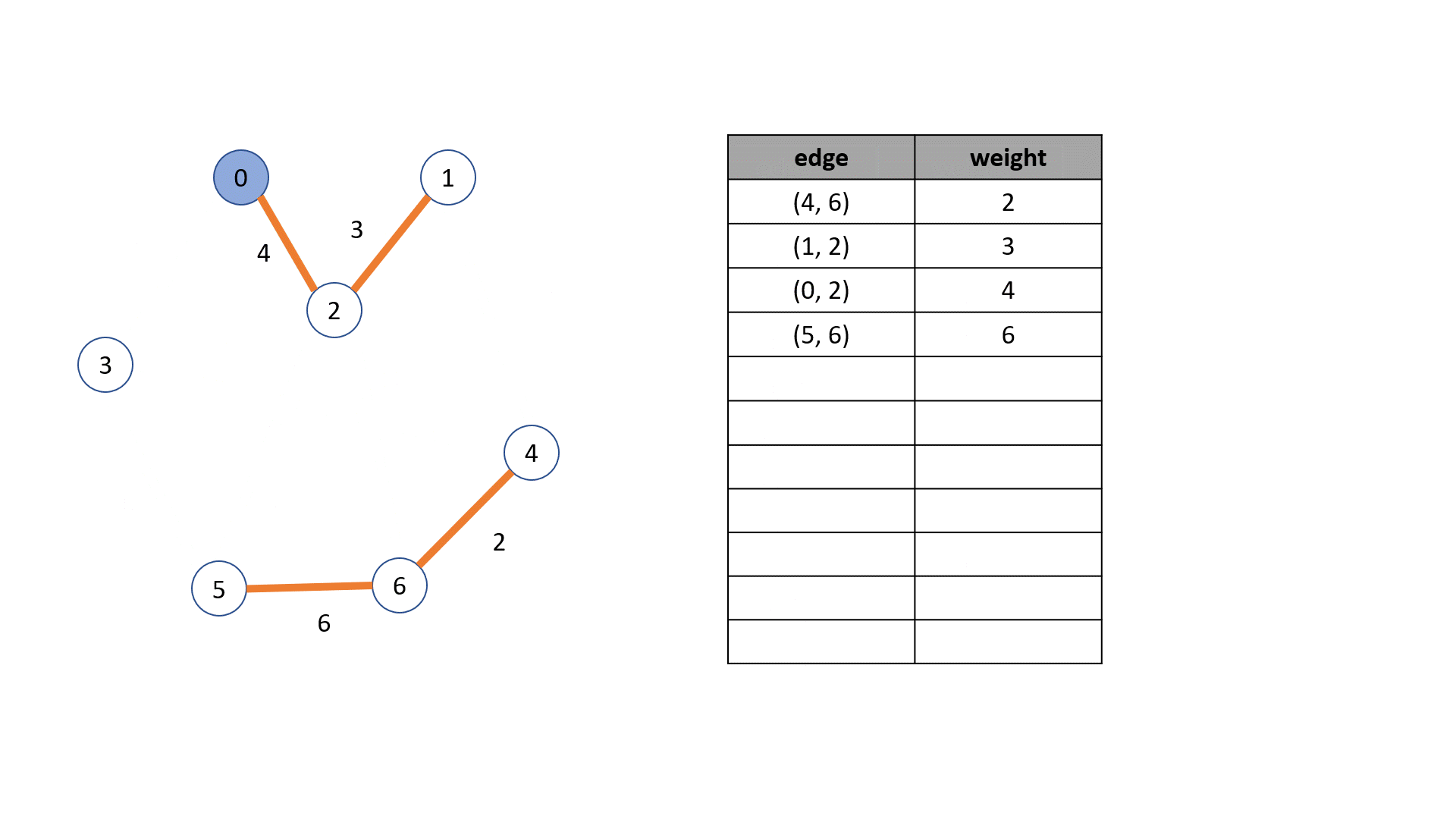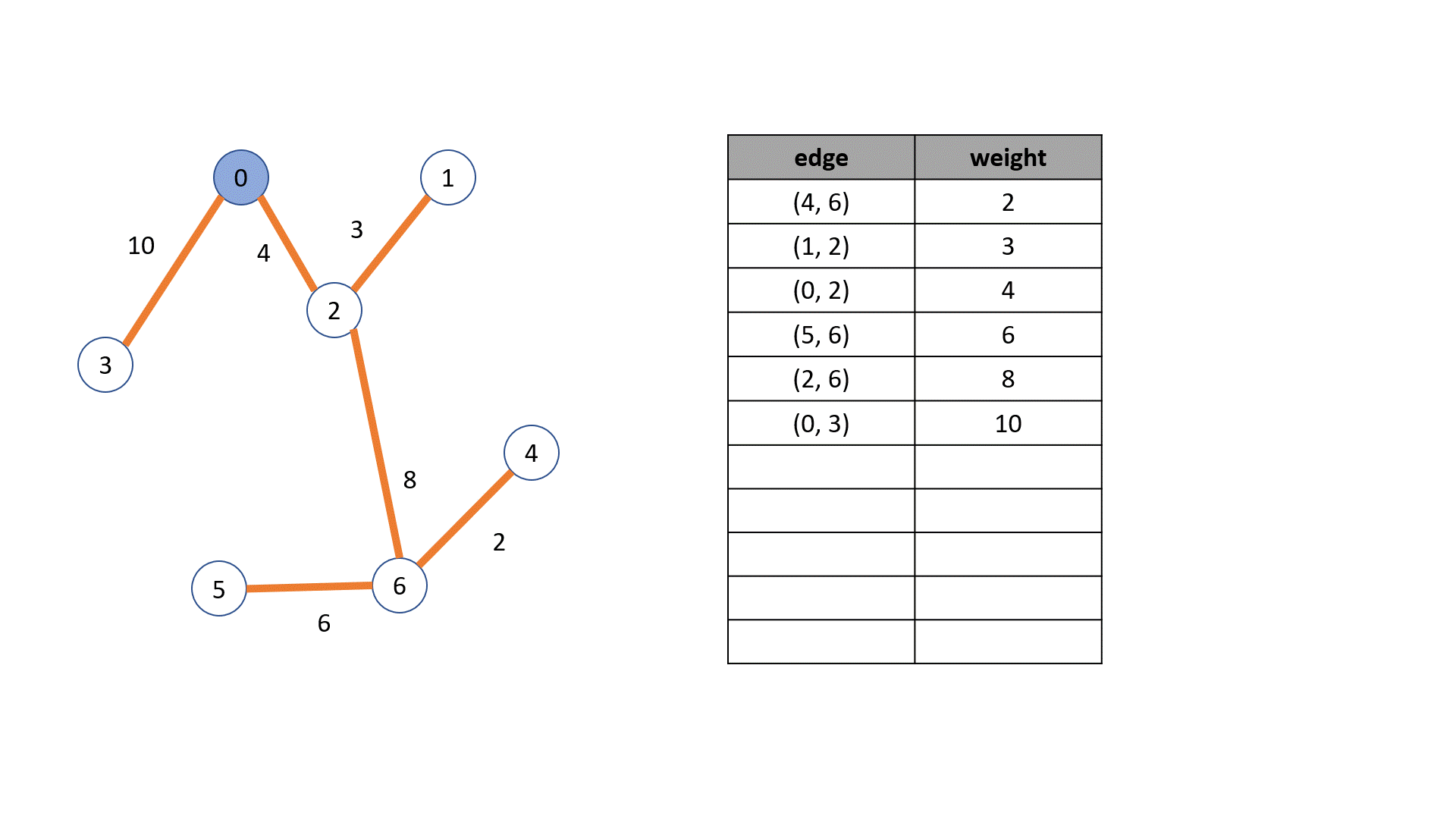
-cycle이 발생하는지 확인하는 방법(무방향 그래프)
- DFS/ BFS
- Union-find(수행시간이 더 효율적임) (무방향 그래프에서만 가능)
-union-find
- Union: v1과 v2가 포함되어 있는 집합을 합치는 연산
- Find : v 가 어떤 집합에 포함되어 있는지 찾는 연산
- 연결되어있는 정점을 같은 집합이라고 본다
- 만약 정점을 연결했는데 같은 부모노드를 공유하고 있다면(같은 집합에 있다면)cycle 발생
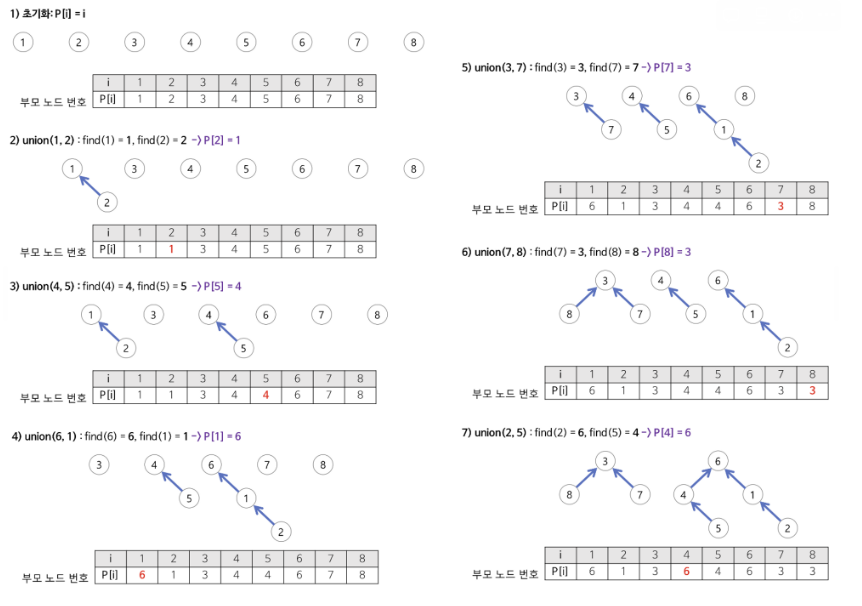
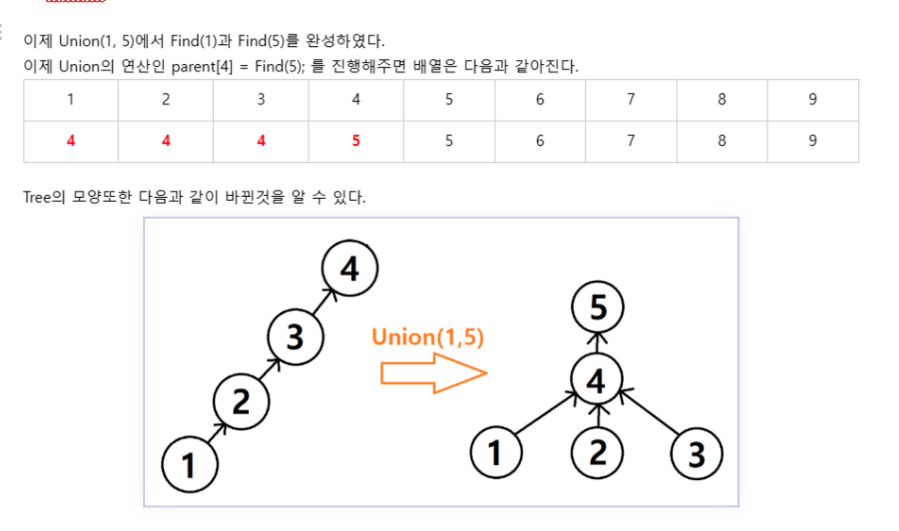
-경로 압축으로 union-find 구현
- 위 예제처럼 경로를 표현하면 vertex를 검사할때마다 계속 부모를 타고 올라가야한다(수행시간 비효율)
코드 구현( java )
import java.io.BufferedReader;
import java.io.FileReader;
import java.io.IOException;
import java.util.Arrays;
import java.util.Comparator;
import java.util.Random;
class EdgeWeight {
int row;
int col;
int weight;
}
public class KruskalAlgorithm {
private static final int max_v = 8;
private static final int max_weight = 1000;
// ... (이전 코드와 동일한 부분)
// 그래프를 랜덤 가중치로 초기화하는 함수
private static void initRandomWeights(int[][] ary) {
Random random = new Random();
for (int i = 0; i < max_v; i++) {
for (int j = i; j < max_v; j++) {
if (i == j) {
ary[i][j] = 0;
} else if (ary[i][j] == 1) {
ary[i][j] = random.nextInt(20) + 1; // 1부터 20 사이의 랜덤 가중치 생성
ary[j][i] = ary[i][j];
} else {
ary[i][j] = max_weight;
ary[j][i] = max_weight;
}
}
}
}
// 가중치 배열 정렬
private static void sort(EdgeWeight[] edgeAry, int n) {
Arrays.sort(edgeAry, Comparator.comparingInt(a -> a.weight));
for (EdgeWeight edge : edgeAry) {
System.out.println(edge.row + "," + edge.col + "," + edge.weight);
}
}
// 경로 압축을 적용한 Find 함수
private static int find(int[] set, int v) {
if (set[v] != v) {
set[v] = find(set, set[v]); // 경로 압축: 부모를 루트로 바로 연결
}
return set[v];
}
// 경로 압축과 높이 기반의 Union 함수
private static void union(int[] set, int[] rank, int n, int v1, int v2) {
int root1 = find(set, v1); // v1의 루트 찾기
int root2 = find(set, v2); // v2의 루트 찾기
if (root1 != root2) { // 서로 다른 집합일 경우에만 합치기
if (rank[root1] < rank[root2]) {
set[root1] = root2; // 대표 노드만 바꾼다
rank[root2] += rank[root1];
} else if (rank[root1] > rank[root2]) {
set[root2] = root1;
rank[root1] += rank[root2];
} else {
set[root1] = root2; // 높이가 같은 경우
rank[root2] += rank[root1];
}
}
}
// 그래프를 인자로 넘기면 최소신장트리를 구성하여 가중치의 합을 구하는 함수
private static void kruskal(int[][] ary, int n) {
EdgeWeight[] edgeAry = new EdgeWeight[n * n];
int count = 0; // edge의 갯수
for (int i = 0; i < n; i++) {
for (int j = i; j < n; j++) { // 무방향이기 때문에 상위 삼각행렬만 검사
if (ary[i][j] > 0 && ary[i][j] < max_weight) {
edgeAry[count] = new EdgeWeight();
edgeAry[count].row = i;
edgeAry[count].col = j;
edgeAry[count].weight = ary[i][j];
count++;
}
}
}
sort(edgeAry, count); // 정렬
int[] vertexSet = new int[n]; // vertex 집합 설정
int[] rank = new int[n]; // 각 집합의 높이(rank) 정보 저장
for (int i = 0; i < n; i++) {
vertexSet[i] = i; // 집합을 자기 자신으로 초기화
rank[i] = 0; // 초기 높이는 0으로 설정
}
int sum = 0; // mst weight sum
for (int i = 0; i < count; i++) { // 간선의 갯수 만큼 반복
if (find(vertexSet, edgeAry[i].row) != find(vertexSet, edgeAry[i].col)) {
// 두 정점의 루트가 다르면 (cycle이 발생하지 않으면)
union(vertexSet, rank, n, edgeAry[i].row, edgeAry[i].col); // 두 정점을 합치기
sum += edgeAry[i].weight; // 연결 후 가중치 합
}
}
System.out.println("MST weight sum: " + sum); // sum 출력
}
public static void main(String[] args) throws IOException {
String filePath = "/Users/aorl2/OneDrive/문서/undirect_graph_data.txt";
int[][] ary = readGraphFromFile(filePath);
adjMatrixDisplay(ary);
kruskal(ary, max_v);
}
}https://www.acmicpc.net/workbook/view/1899
문제집: 크루스칼 (losthistory)
www.acmicpc.net
이미지 출처
[Union-find] 유니온 파인드 - NiklasJang’s Blog
[알고리즘] Union Find 알고리즘 : 경로 압축 (tistory.com)
'cs > 알고리즘' 카테고리의 다른 글
| [알고리즘] DP(Dynamic Programing) 이란 (0) | 2023.08.20 |
|---|---|
| [알고리즘] 버블, 삽입, 퀵 정렬 알고리즘 구현 (java) (0) | 2023.08.20 |
| [알고리즘] 이분 탐색이란(Binary Search) (0) | 2023.08.13 |
| [알고리즘] 브루트 포스 (완전 탐색)알고리즘이란 (0) | 2023.08.13 |
| [알고리즘] 분할 정복이란 (divide conquer) (0) | 2023.08.07 |



