| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 백준 장학금
- JVM
- 이분탐색이란
- 백준장학금
- python
- 프로세스
- 점근적 표기법
- 멀티프로세서
- 자료구조
- 엔티티 그래프
- Kruskal
- 알고리즘
- 연결리스트
- posix
- heapq
- spring
- HTTP
- 연결리스트 종류
- 스케줄링
- 운영체제
- 최소힙
- 완전이진트리
- 강화학습
- AVL트리
- MSA
- jpa n+1 문제
- 힙트리
- JPA
- 최대 힙
- SpringSecurity
- Today
- Total
KKanging
[강화학습] 4. MDP를 알 때의 플래닝 본문
Introduction
- 이번 장은 다음과 같은 상황에서의 문제를 해결한다.
- 작은 문제
- MDP를 알 때
- 이처럼 MDP 에 대한 모든 정보를 알 때 이를 이용하여 정책을 개선해 나가는 과정을 넓게 가리켜 플래닝이라 한다.
- 위와 같이 가장 쉬운 설정에서 정책(파이)가 주어졌을 때 각 상태의 밸류를 평가하는 Prediction 문제
- 최적의 정책 함수를 찾는 Control 문제를 푸는 방법론에 대해 다룬다.
내용은 주로 테이블 기반 방법론에 기반한다.
테이블 기반 방법론이란 모든 상태 s 혹은 상태와 액션의 페어(s,a)에 대한 테이블을 만들어서
값을 기록해 놓고 , 그 값을 조금씩 업데이트하는 방식을 의미한다.
작은 문제에서만 적용 가능하다.
4.1 벨류 평가하기 - 반복적 정책 평가(Prediction)
가정

MDP를 알 때 특정 정책에 대해 각 상태의 가치를 계산해보자.
보상은 스템마다 -1 이라고 하고
정책은 4방향 랜덤으로 간다고 한다(초기 정책)
전이 확률 P는 랜덤으로 간다면 무조건 그 상태로 가기 때문에 100% 이다.
반복적 정책 평가란?
반복적 정책 평가란 테이블의 값들을 초기화한 후, 벨만 기대 방정식을 반복적으로 사용하여
테이블에 적어 놓은 값을 조금씩 업데이트해 나가는 방법론이다.
1. 테이블 초기화

일단 각 상태의 가치를 0으로 초기화 한다.
(0이 아닌 값도 되지만 정답과 멀수록 업데이트 횟수가 많아지기도 하고 지금은 정답을 모르기에
적당한 값인 0으로 초기화한다)
2. 한 상태의 값을 업데이트

벨만 기대 방정식을 이용하여 계산한다.
정책의 값은 0.25로 동일한 확률 4개가 존재하고
감마는 1로 한다.(설정)
보상은 -1로 (고정)
전이 확률은 100퍼센트이기 때문에 1을 곱한다.(고정)

3. 모든 상태에 대해 2의 과정을 적용

4. 앞의 2~3 과정 반복

벨만 기대 방정식을 이용해 업데이트를 계속해서 실제 가치를 알 수 있음
과연 각 상태의 가치는 정확한 값일까?

물론 초기 상태의 가치는 임의 값이지만 위에 벨만 방정식을 보면 임의값에 환경이 주는 실제 값을
업데이트 하는 개념이다.
따라서 업데이트 초기에는 의미 없는 상태 값일지 몰라도 반복적으로 개선한다면
의미있는 가치 값이 된다.
위에 예제를 보면 목표 상태(0)에서 점차적으로 퍼지는 것을 볼 수 있다.
최고의 정책 찾기
본 챕터에서는 MDP를 알 때 최적의 정책을 찾는 2가지 방법을 배워봅니다.
1. 정책 이터레이션
2. 벨류 이터레이션
4.2 최고의 정책 찾기 - 정책 이터레이션
- 정책 평가와 정책 개선을 번갈아 수행하여 정책이 수렴할 때까지 반복하는 방법론
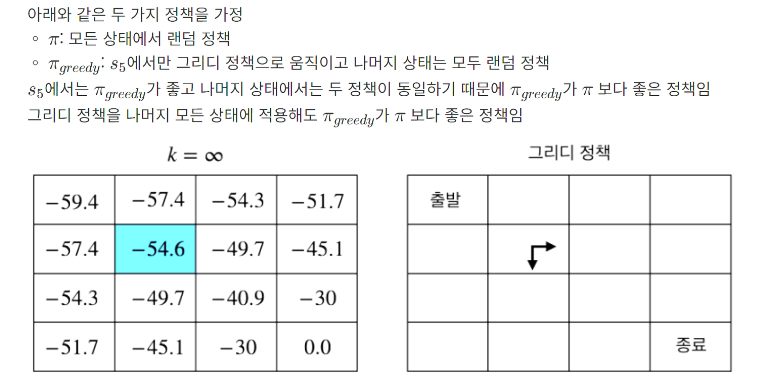
- 예제

위 상태에서 최적의 정책은 무엇일까?
먼 미래를 보지 않고 바로 다음 가치가 높은 동쪽과 남쪽으로 가는 것이다.

그리디 정책

그리디 정책이란 : 먼 미래를 생각하지 않고 다음 칸의 가치가 가장 큰 것을 선택하는 것
*위에는 한번의 가치 평가만으로 정책이 많이 개선되었지만 이건 문제가 작고 간단하기 때문이다.*
평가와 개선의 반복
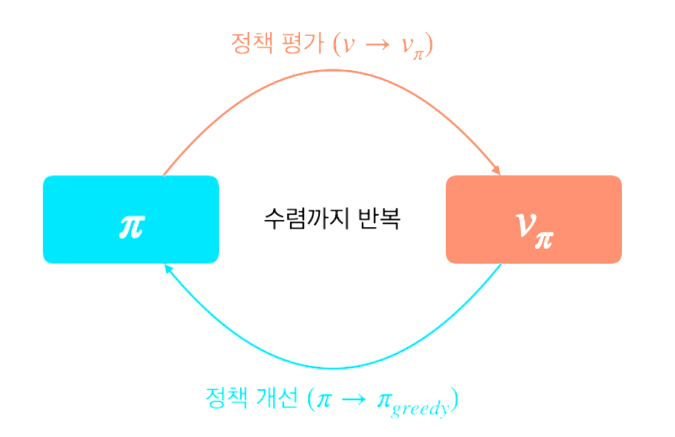
위에 반복적 정책 평가(Prediction)를 통해서 정책에 대한 평가를 하였다
그리고 주어진 가치에 대해 그리디 정책을 이용한 정책 이터레이션을 통해 정책을 개선을 하였다.
이 과정을 반복하여 최적의 정책을 구해 나간다.
그러다 보면 정책의 값도 변하지 않고 가치도 변하지 않게 되면 그 때는 최적의 정책과 최적의 가치가
된다.
과연 정책은 개선되는가?
정책 평가 부분 간소화하기

정책 평가와 정책 개선의 반복을 통해 최적 정책을 도출한다는 것은 이해가 됐을 것이다.
하지만 위에 예시처럼 정책 평가 부분을 무한대로 반복할 수 있을까?
그리고 이중 반복문 형태이기 때문에 수행시간 또한 기하급수적이다.
이를 간소화하기 위해 시간이 많이 드는 정책 평가 부분을 간소화 해보자.
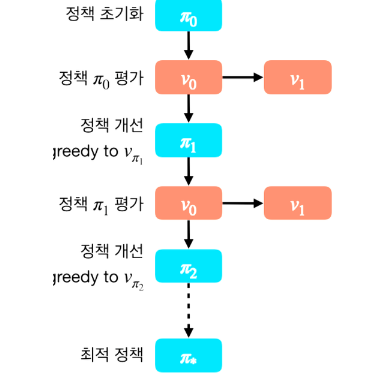
일찍 멈춰(early stopping)을 통해 정책 평가를 무한대로가 아닌 짧은 반복만하고 멈춰 버리는 것
그리디 월드 같은 간단한 문제는 1번의 반복 만으로도 정책이 개선 가능하다.
-> 우리의 목적은 최고의 정책을 찾는 것이지,
정확한 가치를 평가하는 것은 아니다.
4.3 최고의 정책 찾기 - 벨류 이터레이션
정책 이터레이션은 한번의 반복에 다른 정책이 나왔다.
하지만 벨류 이터레이션은 최적의 정책이 만들어 낸 최적 밸류 하나만을 보고 따라간다.

최적의 정책을 활용하므로 벨만 기대 방정식이 아닌 벨만 최적 방정식을 활용한다.

- 반복적으로 구한 결과
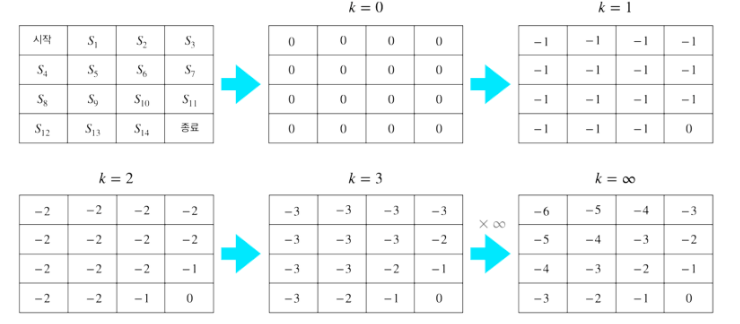
우리가 구하고 싶은 것은 최적 벨류가 아닌 정책에 대한 벨류이다.
근데 최적 벨류를 왜 구했을까
MDP를 아는 상황에서는 최적 벨류를 알면 최적 정책 또한 알 수 있기 때문이다.
'인공지능 > Reinforcement Learning' 카테고리의 다른 글
| [강화학습] 5. MDP를 모를 때 밸류 평가하기 (0) | 2024.05.20 |
|---|---|
| [강화학습] 3. 벨만 방정식 (0) | 2024.05.09 |
| [강화학습] 2. 마르코프 결정 프로세스 (0) | 2024.05.05 |
| [강화학습] 1. 강화학습이란 (0) | 2024.05.04 |




