
벨만 방정식이란?


2장에서 MDP 를 설계하는 방법을 배우고 다음이 강화학습의 목적이란 것을 배웠다.
S : 상태의 집합
A : 는 액션의 집합
P : 어떤 상태 St 에서 a 행동을 했을 때 다음 상태 St+1로 전이할 전이 확률 행렬
R : MDP에서는 해당 s 에서 특정 행동 a를 했을 때의 보상 함수.
감쇠 인자 감마
정책 함수 : 어떤 상태 s에서 취할 수 있는 액션 중 어떤 액션을 선택할지 정해주는 함수
강화학습은 최종 보상을 최적화 하는 정책함수를 찾는 것이다.
정책함수를 찾기 위해서는 주어진 정책함수에서 상태별 벨류를 찾아야 한다.
벨류를 계산한다는 건 벨만 방정식을 이용해서 구한다로 변경해도 된다.
벨만 방정식이 무엇인지 알아보자
3.1 벨만 기대 방정식
0 단계

상태(St)에 대한 벨류를 다음 상태(St+1) 의 벨류에 대해 구한 재귀식


벨만 방정식 0 단계의 식이다.
상태 St 에 대한 가치를 나타내는 벨만 방정식인데
E[Gt] 로 표현하였다 (E는 기댓값)
Gt(리턴 함수) 의 기댓값이 St의 벨류이다.
이것을 조금 더 풀어서 설명하면
다음 상태로 가는 행동을 하고 그 행동에 대한 보상(r t+1) + 다음 상태에 대한 벨류의 합으로
구할 수 있다
그럼 위에 식의 의미를 알 수 있다.
0단계 : 기댓값인 이유

왜 상태에 대한 벨류는 리턴의 기댓값일까 그냥 벨류 = 리턴은 안되는 것일까

이유는 다음과 같다.
MDP의 요소 ( S,A,R,P,감마) 는 환경의 요소이다.(즉 agent가 조작 불가능)
하지만 각 상태에서 행동을 취하는 확률인 (정책함수 파이) 는 agent의 영역이다.
위에 예제로 본다면 St에서 다음 상태로 전이되는 연산은 2가지로 거쳐서 구해진다.
Agent가 상태 St에서 정책함수의 의해 행동 a를 선택한다(Agent 영역)
그다음은 전이확률 행렬 P에 의해 상태가 변경 된다.(환경)
위와 같이 2가지의 확률 연산을 거쳐야만 다음 상태를 구할 수 있게된다.
따라서 상태 St의 벨류는 확률적으로 4가지 상태 중 하나(위 예제 기준)가 선택 되어야 해서
기댓값 연산자가 없다면 벨만 방정식의 0단계는 성립하지 않는다.
1단계
1단계는 상태(St)에서 수행한 액션(a)에 관한 액션 가치 함수를 나타내는 수식이다.
액션 가치 함수는 q로 쓴다.
1단계 : q를 이용해 v 계산하기

만약 정책함수와 액션 가치 함수를 알고 있다면
상태 가치 함수를 구할 수 있다.
식은 위와 같다
- 구하는 예제

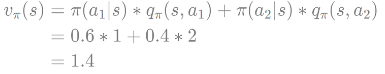
액션 가치 함수를 알고 있으면 상태 가치 함수를 구할 수 있음
1단계 : v를 이용해 q 계산하기

- 위 식은 아래의 예제로 이해 가능
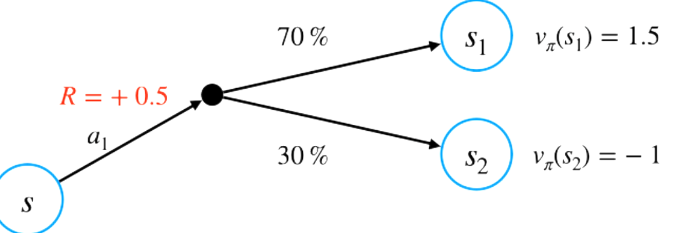
- 액션 a1에 대한 보상 r , 상태전이 확률 p , 상태 밸류 v(s1)과 v(s2) 알고 있다고 가정 하면 상태 s에서 액션 a의 밸류 계산 가능
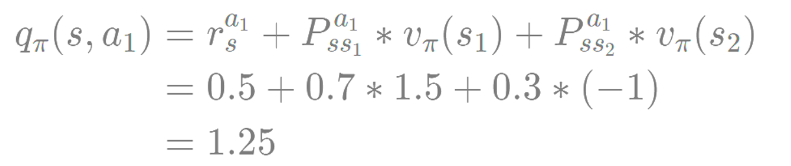
2단계
- 1단계 q 에 대한 식을 v 에 대한 식에 대입하면 아래와 같음
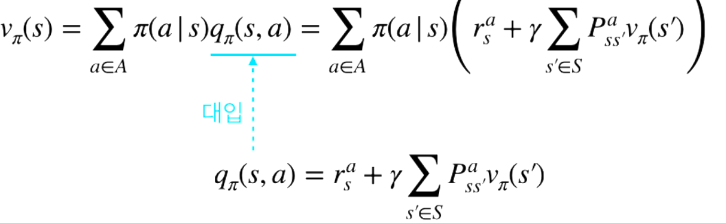
- 반대로 v에 대한 식을 q에 대입하면 아래와 같다
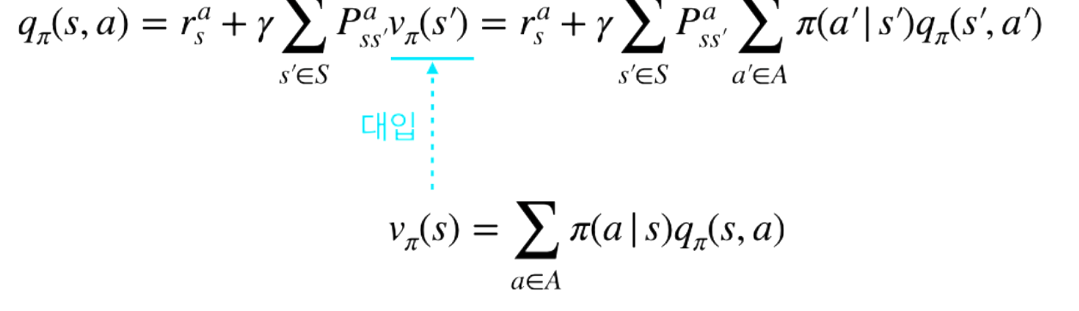
v(s) 에 대한 벨만 방정식 정리
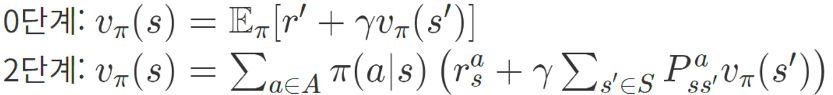
2단계 식을 계산하기 위해서는 다음 2가지를 반드시 알아야 한다.
1. 보상함수 r
2. 전이 확률 P
위 2개를 안다는 건 MDP를 안다고 봐도 무방하다.
하지만 MDP를 모르는 상황에서는 2단계 식이 아닌 0단계 식을 구해야하고
실제로는 대부분의 경우 MDP를 모르기 때문에 경험(experience)을 통해 학습한다.
모델 프리 : MDP를 모를 때 학습하는 접근법
모델 베이스 : MDP를 알고 있을 때 학습하는 접근법
3.2 벨만 최적 방정식
최적 벨류와 최적 정책
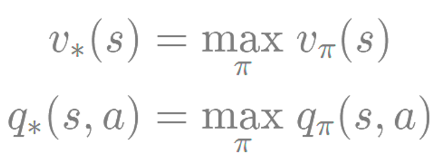
벨만 기대 방정식은 특정 정책에 대한 벨류에 관한 방정식이었다면
벨만 최적 방정식은 최적 정책에 따른 최적 벨류에 관한 방정식이다.
즉, 어떤 MDP가 주어졌을 때 , 그 MDP 안에 존재하는 모든 파이들 중에서 가장 좋은 파이를 선택하여
계산한 벨류가 곧 최적 벨류라는 뜻이다.
최적 정책의 정의

어느 정책이 더 좋은가??
>>> 대소 관계로 벨류 값 비교
모든 상태에 대해 적용되는 가장 좋은 정책이 존재하는가?
>존재하지만 이는 수학자들의 정의에 의해 구해졌는데 책의 범위가 아니라 생략하겠다.
최적 벨류의 정의

최적 정책이 정의되면 최적 벨류는 위와 같이 정의된다.
벨만 최적 방정식
벨만 기대 방정식은 벨류를 구하기 위해 2가지 확률적 요소가 존재했다.
정책에 대한 확률, 전이 확률
따라서 정확한 상태를 구할 수 없으므로 벨만 기대 방정식의 식에는 기댓값이 많이 들어갔다.
하지만 벨만 최적 방정식은 최적의 정책을 구했으므로 특정 상황에서의 액션은 정해져 있다.
최적 방정식은 액션을 선택할 때 확률적으로 선택하는 것이 아니라 최댓값 연산자를 통해
제일 좋은 액션을 선택하기 때문에 최댓값 연산자를 많이 사용한다.
아직 전이 확률에 대한 확률적 요소가 있기 때문에 기댓값 연산자 또한 사용한다.
0단계
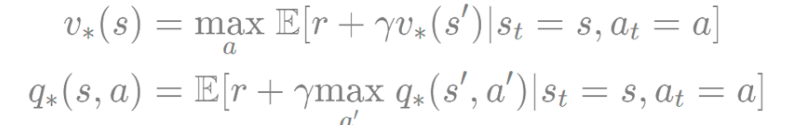
벨만 기대 방정식은 기댓값 E에 파이 연산자도 붙였었지만 벨만 최적 방정식은
위 기댓값의 값을 최적으로 해주는 a 를 선택했기 때문에 E에 첨자 파이가 제거 되었다.
아직 확률적 요소인 전이 확률이 남아 있기 때문에 E는 제거 되지 않았다
1단계
- q 를 이용해 v 계산하기**
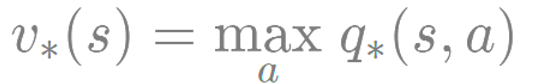
q* 를 이용해 v*를 구하는 것은 간단하다.
쉽게 상태 s의 최적 벨류는 s에서 선택할 수 있는 액션들 중에 벨류가 가장 높은 액션의 벨류와 같다는
뜻이다.
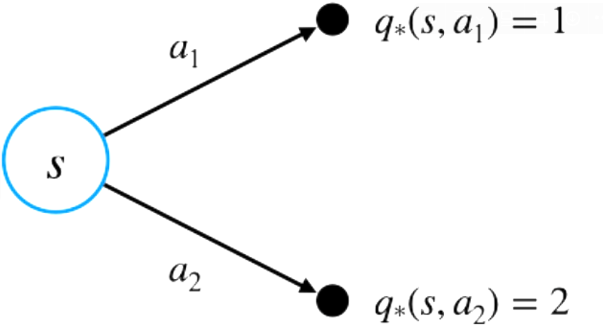
위 그림에서 최적 액션은 두 개의 액션 중 가치가 높은 a2를 선택하는 것
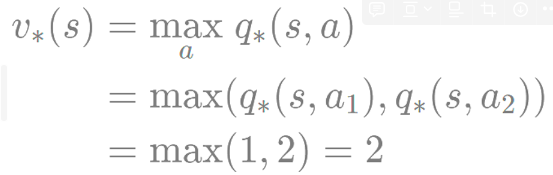
- v를 이용해 q 계산하기
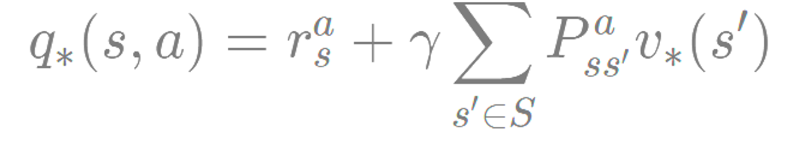
2단계
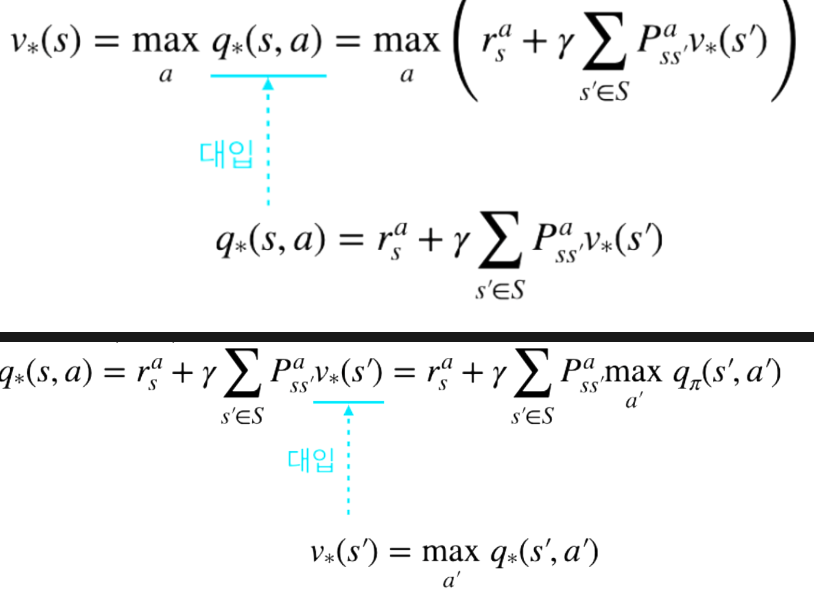
요약
강화학습에서 벨류는 중요하다.
정책 파이를 평가하고 싶다면 벨만 기대 방정식을
최적의 벨류를 찾는 일을 할 때에는 벨만 최적 방정식을 사용하여 해결해야 한다.
참고 도서
- 바닥부터 배우는 강화학습
'인공지능 > Reinforcement Learning' 카테고리의 다른 글
| [강화학습] 5. MDP를 모를 때 밸류 평가하기 (0) | 2024.05.20 |
|---|---|
| [강화학습] 4. MDP를 알 때의 플래닝 (0) | 2024.05.12 |
| [강화학습] 2. 마르코프 결정 프로세스 (0) | 2024.05.05 |
| [강화학습] 1. 강화학습이란 (0) | 2024.05.04 |
