| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- heapq
- 운영체제
- 연결리스트 종류
- jpa n+1 문제
- 알고리즘
- JVM
- MSA
- 최소힙
- 멀티프로세서
- HTTP
- 연결리스트
- 프로세스
- 백준장학금
- 스케줄링
- spring
- SpringSecurity
- 완전이진트리
- 점근적 표기법
- python
- 백준 장학금
- Kruskal
- posix
- 강화학습
- 자료구조
- 이분탐색이란
- 엔티티 그래프
- 최대 힙
- JPA
- 힙트리
- AVL트리
- Today
- Total
KKanging
[강화학습] 5. MDP를 모를 때 밸류 평가하기 본문
Preview(이때까지 배운 것들)

- 해결하고 싶은 문제의 도메인을 MDP 형식에 맞게 문제를 정의하는 법을 배웠다.


- 벨만 기대 방정식과 벨만 최적 방정식을 이용하여 해당 상태와 행동에 대한 가치를 구할 수 있었다.

- MDP를 알고 문제의 size가 작은 문제를 해결하는 방법을 배웠다.
- 벨류 평가하기 - 반복적 정책 평가
- 최고의 정책 찾기
- 정책 이터레이션
- 벨류 이터레이션
MDP를 모를 때 밸류 평가하기
모델 프리란

MDP를 모른다는 것은 정확하게 보상함수와 전이 확률을 모른다는 의미이다.
이런 상황을 모델 프리라고 한다.
-> 여기서 모델은 Agent 가 행동을 했을 때 환경이 어떻게 응답할지 알려주는 모든 것을 의미하는
model of environment의 줄임말이다.
즉 모델을 모른다. MDP를 모른다. 모델 프리다는 같은 의미로서 인식하면 된다.
뭐가 달라졌을까

MDP를 알때는 Agent가 행동에 대해 리턴값과 어떻게 이동될지 알 수 있다는 의미이다.
그래서 MDP를 알때는 플래닝을 통해서 정책의 가치를 알 수 있었다.
하지만 이제는 가치함수와 전이 확률을 못쓰기 때문에 2단계를 못쓴다.
하지만 MDP를 모르므로 임의의 확률이 실제 확률에 근접할 때까지 실행해봐야 한다.
몬테카를로 학습
간단한 예제 ( 동전 던지기)

동전 던지기라는 액션을 했을 때 동전의 면이 나올 확률을 모른다고 가정해보자 (실제 확률은 50:50)
만약 10번 던져서 3번이 앞면이 나온다면
이 동전의 기댓값은 대충 30% 로 앞면이 나온다는 것을 알 수 있다.
만약 10번으로 부족하다면 100번 던져봤을 때 35번 앞면이 나왔다면 앞면의 기댓값은 35%가 될 것이다.
여러번 던질 수록 실제 기댓값과 같아 질 것이고 이게 몬테카를로 학습의 기본 철학이다.
5.1 몬테카를로 학습이란
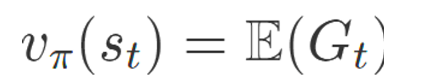
특정 상태 St 의 벨류 평가를 위해 해당 상태의 리턴 값 즉 Gt 의 기댓값으로 알 수 있었다.
리턴값은 한 에피소드가 끝났을 때 각 상태의 리턴 값을 의미하고
많은 에피소드 반복을 통해 구한 리턴 값의 평균이 곧 "상태의 기댓값" => "상태의 밸류" 이다.
이렇게 구한 상태의 밸류는 대수의 법칙의 의해 에피소드 반복 수 만큼 더 정확해 진다.
몬테카를로 학습 알고리즘(그리드 월드)
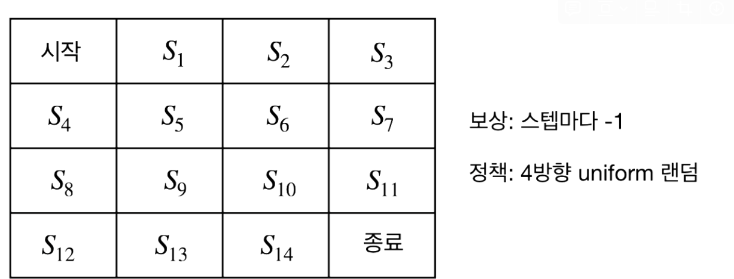
- 플래닝과 달라진점
MDP를 알때와 같이 보상 함수와 전이확률은 이미 정해져 있다.
하지만 다른 점은 보상함수와 전이확률을 정확히 모른다는 가정이다.
MDP를 알 때는 계획(플래닝) 을 통해서 행동의 따른 결과를 예측할 수 있었다.
하지만 MDP를 모르기 때문에 직접 실행을 통해서만 가치를 구할 수 있다.
"즉 경험을 통해서만 상태의 전이와 보상을 알 수 있고 사전에 상태의 가치를 판단할 수 없다는 것을 의미"
- 테이블 초기화
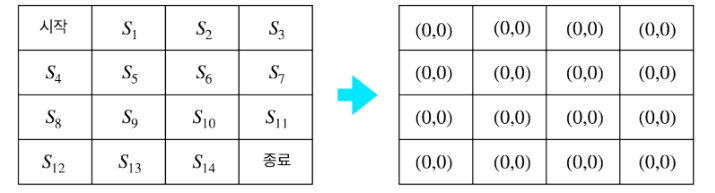

2. 경험 쌓기
- 에이전트가 시작 S0 에서 시작해서 종료 ST에 도달하기까지의 에피소드를 실행
상태 → 액션 → 보상
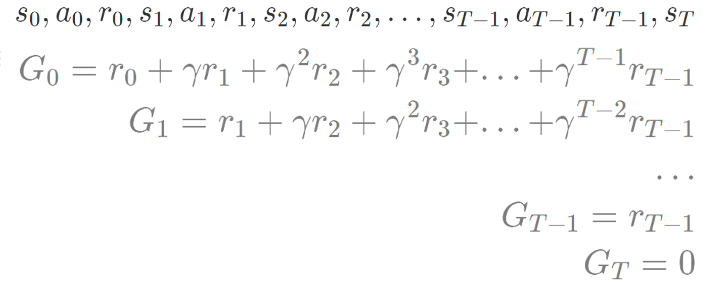
3. 테이블 업데이트
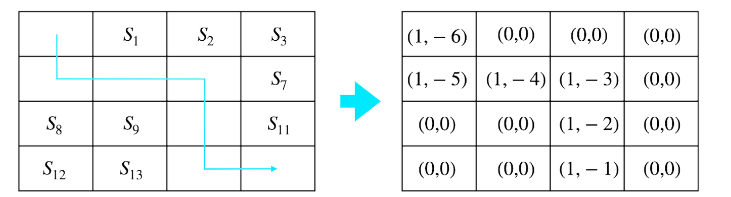
- 만약 다음과 같이 에피소드 진행되었다고 가정
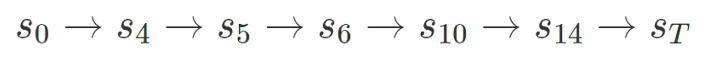
- 방문 했던 모든 상태에 대해 값 업데이트
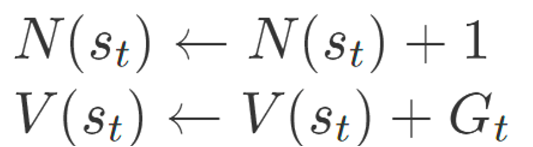
4. 밸류 계산
• 많은 횟수의 에피소드를 경험 후 충분히 경험이 쌓이면 리턴의 평균을 밸류의 근사치로 사용
• 이와 같이 많은 에피소드를 통해 밸류를 추정하는 방식이 몬테카를로 방법론
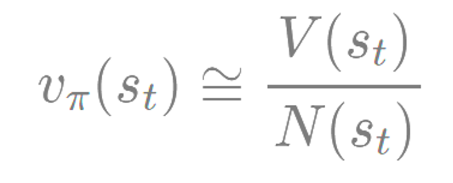
위처럼 기대값을 구한다면 에피소드의 총 횟수를 다 수행한 후에야 가치를 업데이트 한다.
조금씩 업데이트하는 버전

- 에피소드가 1개 끝날 때마다 테이블의 값을 조금씩 업데이트
- α는 얼마큼 업데이트할지 크기를 결정해주는 파라미터
- N(st)에 값을 따로 저장해 둘 필요 없이 에피소드가 끝날 때마다 테이블의 값을 업데이트
- 아래와 같음
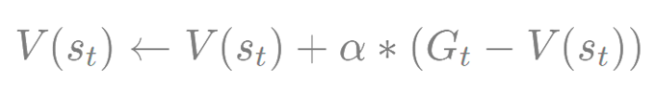
에피소드가 끝나기 전에 업데이트 할 수 없을까?
만약 금요일에 일요일 강수확률을 구하는 것이 더 정확할까
아님 토요일에 일요일 강수확률을 구하는 것이 정확할까
-> 당연히 토요일에 일요일 강수확률을 구하는 것이 정확하다.
MC 와 TD(Temporal Difference) 와 비교한다면
MC 는 일요일까지 가서야 금요일의 일요일 강수확률을 업데이트 한다.
TD 는 토요일(금요일에 다음 스텝)의 일요일 강수확률을 기반으로 금요일의 강수 확률을 업데이트한다.
이와 같이 "TD는 미래의 추측으로 과거의 추측을 업데이트 하는 방식이다."
그래서 TD 는 이름이 시간적 차이이다.
- 이론적 배경
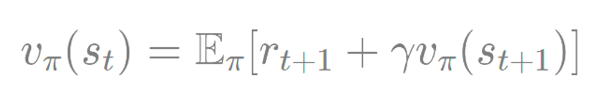
벨만 기대 방정식 0 단계를 t+1 스탭 (다음 스탭) 을 정하면 위와 같은 식의 기댓값으로 변형 가능하다.
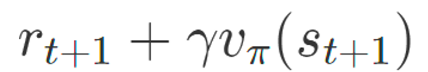
위 식을 여러 번 뽑아서 평균을 내면 그 평균이 상태 가치에 수렴하게 된다.
*용어 정리
TD 타깃 : 위의 식
Temporal Difference 학습 알고리즘
- TD도 MC와 마찬가지로 테이블 값을 0으로 초기화
- TD와 MC의 차이는 업데이트 수식과 업데이트 시점이 다름
- 아래의 에피소드를 가정
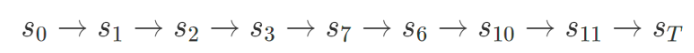
- TD는 각각의 상태 전이가 일어나자마자 바로 테이블의 값을 업데이트

• 테이블의 값이 수렴할 때까지 진행
5.3 MC vs TD
- 여러 측면에서 MC와 TD 를 비교
학습 시점

편향성(Bias)

편향되지 않는 다는 것은 이상한 곳으로 기울지 않은 올곧은 추정량이라는 의미이다.
따라서 MC에서 리턴의 기댓값은 많이 반복할수록 실제 가치함수에 근접할 수 있는 것이다.

TD에서 V(st+1) 은 테이블에 담겨져 있는 값일 뿐 실제 값과는 차이가 있다 따라서
TD는 편향되어 있음을 알 수 있다.
- 그럼 TD는 편향되어 있으니 안좋은걸까?
TD는 편향되어 있긴 하지만 여러가지 조건(TD-zero와 같은)이 붙으면 TD 타깃이 불편 추정량이라는
정리가 있기도 하고
실제로 size가 커지서 뉴럴넷을 이용하면 불편 추정량을 보장하지 않지만 매우 좋은 성능을 보인기도
한다.
분산(Variance)
- MC는 에피소드가 끝나야 하기 때문에 리턴이 -6 또는 -2000 등 다양한 값을 가질 수 있음. **분산(variance)**이 큼
- TD는 한 샘플만 보고 업데이트하기 때문에 분산이 작음
5.4 몬테카를로와 TD의 중간
- MC 와 TD의 장단점을 알았다 근데 두 학습 방법 밖에 없을까? 그 중간은 없을까?
n스텝 TD
n스텝 TD 이란 : TD에서 n 스텝을 진행하고 난 뒤 추측 치를 이용
위에서 TD 개념에서 더 종료 지점과 근접하면 추정 확률이 높아진다고 알고 있다. 그래서 바로 앞 스텝이 아닌 N개의 스텝의 추측 치를 이용하는 것
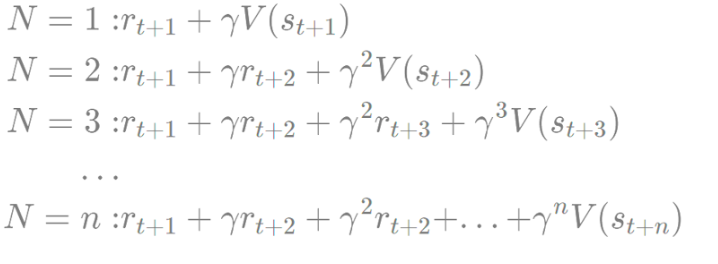
스텝을 무한으로 간다면 (종료 시점을 T로 가정)
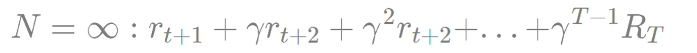
- 위 값은 리턴임. 즉 MC는 TD의 한 사례
- TD(0): N=1인 경우의 TD를 TD-zero라고 함
- N이 커질수록 bias는 줄어들고 variance는 커짐
- TD(0)와 MC 사이의 적당한 구간을 찾는 것은 어려운 문제
코드
Agent
import random
class Agent():
def __init__(self):
pass
def select_action(self):
coin = random.random()
if coin < 0.25:
action = 0
elif coin < 0.5:
action = 1
elif coin < 0.75:
action = 2
else:
action = 3
return action
GridWorld
import random
class GridWorld():
def __init__(self,grid_size):
self.x = 0
self.y = 0
self.grid_size = grid_size
def step(self, a):
if a == 0:
self.move_right()
elif a == 1:
self.move_left()
elif a == 2:
self.move_up()
elif a == 3:
self.move_down()
reward = -1
done = self.is_done()
return (self.x, self.y), reward, done
def move_right(self):
self.y += 1
if self.y > self.grid_size-1:
self.y = self.grid_size-1
def move_left(self):
self.y -= 1
if self.y < 0:
self.y = 0
def move_up(self):
self.x -= 1
if self.x < 0:
self.x = 0
def move_down(self):
self.x += 1
if self.x > self.grid_size-1:
self.x = self.grid_size-1
def is_done(self):
if self.x == self.grid_size-1 and self.y == self.grid_size-1:
return True
else:
return False
def get_state(self):
return (self.x, self.y)
def reset(self):
self.x = 0
self.y = 0
return (self.x, self.y)
MC
from agent import Agent
from gridworld import GridWorld
import math
import time
def main():
# 실험 변수
data_n = 4 # grid size
print_n = 5000 # 출력 주기
env = GridWorld(data_n)
agent = Agent()
data = [[0.0] * data_n for _ in range(data_n)]
gamma = 1.0
alpha = 0.0001
for k in range(1):
done = False
history = []
while not done:
action = agent.select_action()
(x, y), reward, done = env.step(action)
history.append((x, y, reward))
env.reset()
cum_reward = 0 #Gt
for transition in history[::-1]: #뒤부터 계산
x, y, reward = transition
data[x][y] = data[x][y] + alpha * (cum_reward - data[x][y])
cum_reward = reward + gamma * cum_reward #Gt = R(t+1) + gammaG(T+1)
if k % print_n == 0:
print("epoch: ",k,"-----------------")
for row in data:
print(row)
print("epoch: ",k,"-----------------")
for row in data:
print(row)
if __name__ == "__main__":
start = time.time()
main()
end = time.time()
print(f"{end - start:.5f} sec")
TD
from agent import Agent
from gridworld import GridWorld
import math
import time
def main():
# 실험 변수
data_n = 4 # grid size
print_n = 5000 # 출력 주기
env = GridWorld(data_n)
agent = Agent()
data = [[0.0] * data_n for _ in range(data_n)]
gamma = 1.0
alpha = 0.01
for k in range(50000):
done = False
while not done:
x, y = env.get_state()
action = agent.select_action()
(x_prime, y_prime), reward, done = env.step(action)
x_prime, y_prime = env.get_state()
data[x][y] = data[x][y] + alpha*(reward+gamma*data[x_prime][y_prime]-data[x][y])
if k % print_n == 0:
print("epoch: ",k,"-----------------")
for row in data:
print(row)
env.reset()
print("epoch: ",k,"-----------------")
for row in data:
print(row)
if __name__ == "__main__":
start = time.time()
main()
end = time.time()
print(f"{end - start:.5f} sec")
참고 문헌
'인공지능 > Reinforcement Learning' 카테고리의 다른 글
| [강화학습] 4. MDP를 알 때의 플래닝 (0) | 2024.05.12 |
|---|---|
| [강화학습] 3. 벨만 방정식 (0) | 2024.05.09 |
| [강화학습] 2. 마르코프 결정 프로세스 (0) | 2024.05.05 |
| [강화학습] 1. 강화학습이란 (0) | 2024.05.04 |




