250x250
Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
Tags
- heapq
- jpa n+1 문제
- 힙트리
- Kruskal
- python
- posix
- 멀티프로세서
- AVL트리
- 운영체제
- 점근적 표기법
- MSA
- JVM
- HTTP
- spring
- 엔티티 그래프
- 프로세스
- 이분탐색이란
- 백준장학금
- 최소힙
- 알고리즘
- JPA
- 강화학습
- 백준 장학금
- 연결리스트 종류
- 연결리스트
- 최대 힙
- 자료구조
- SpringSecurity
- 스케줄링
- 완전이진트리
Archives
- Today
- Total
KKanging
[알고리즘]DFS/BFS(그래프 탐색 알고리즘) 개념과 구현(JAVA) 본문
우선 그래프 이론과 큐와 스택을 모른다면
스택 을보고 오시기 바랍니다.
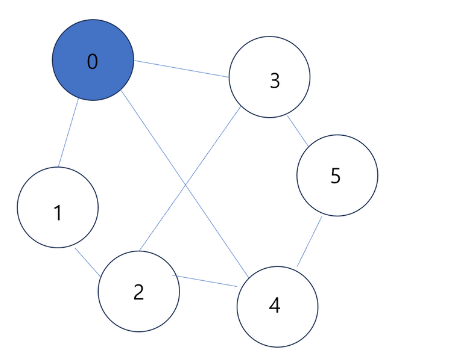
그래프를 탐색하는 방법
- DFS (깊이 우선 탐색)
- BFS (너비 우선 탐색)
DFS(Depth-First-Search)
- 관련 있는 노드를 최대한 깊이 있게 탐색하는 방법
- 구현 방법
- stack
- 재귀함수
구현 방법

- 우선 방문한 정점을 다시 방문하는 일이 없도록 visited 배열을 만들어 준다.
- 0은 아직 방문하지 않았다는 의미
- 시작 정점 하나부터 stack에 넣는다.

- <핵심 로직>
- 그리고 stack의 있는 원소를 pop 한다
- pop 된 정점과 연결되어 있는 정점을 stack에 push 한다.
- pop 된 정점과 연결되어 있는 visited 원소를 1로 바꾼다.
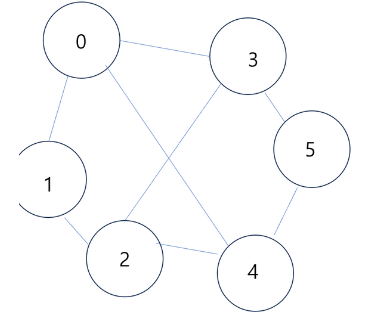
- 이제 핵심 로직을 반복하면 된다.
- 4가 pop 되고 4와 연결되어 있는 정점을 찾을 것이다.
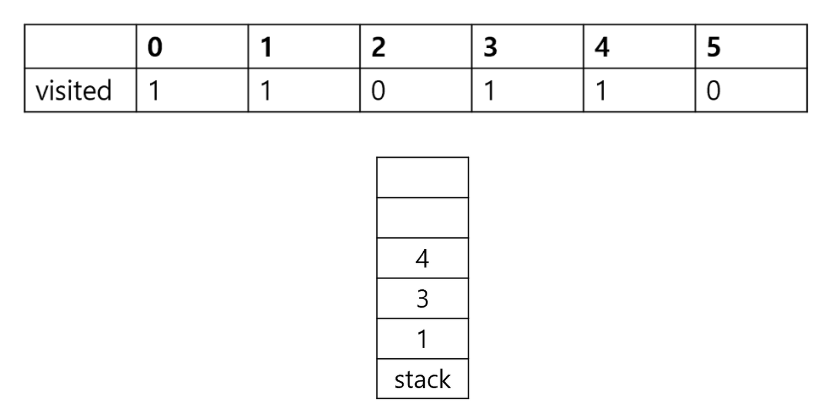
- 4와 연결되어있는 정점은 0 ,2 , 5이다.
- 여기서 0과 2는 이미 방문한 정점이므로 stack에 넣지 않는다.
- 그리고 4와 연결되어 있는 정점 1로 바꿔주면 된다.
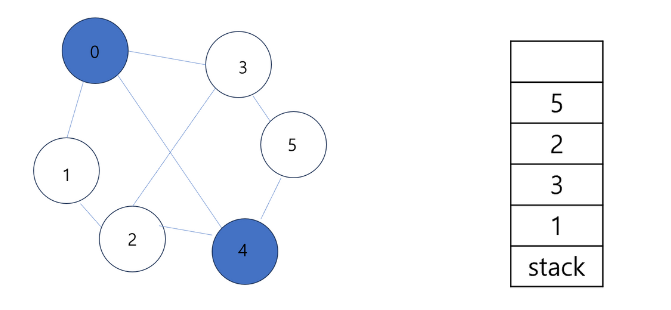
이제 5가 pop 되고 위 로직을 반복하면 된다.
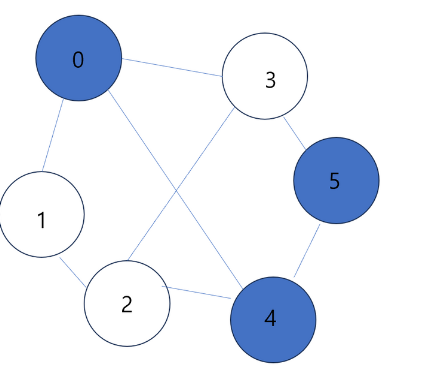
- 5는 더 이상 방문되지 않은 정점을 방문할 수 없다.
- 그래서 5에서 더 이상 나갈 수 없으므로 백트래킹을 한다.
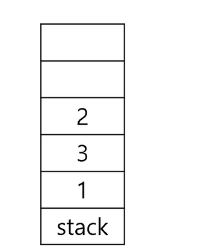
다시 4 정점과 열결 된 2 정점으로 탐색을 할 것이다(stack의 top이 2이기 때문)
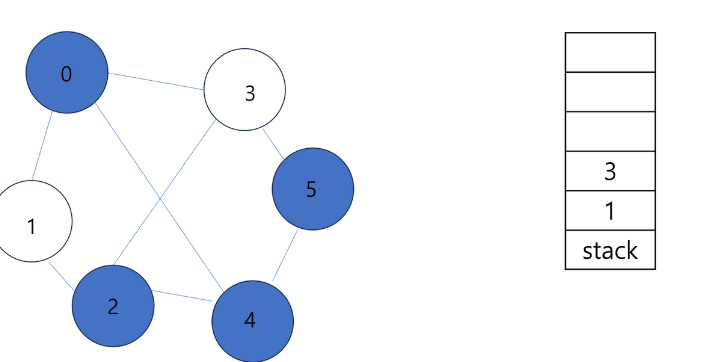
3 도 더 이상 방문할 수 없고 1도 더이상 방문할 수 없기 때문에
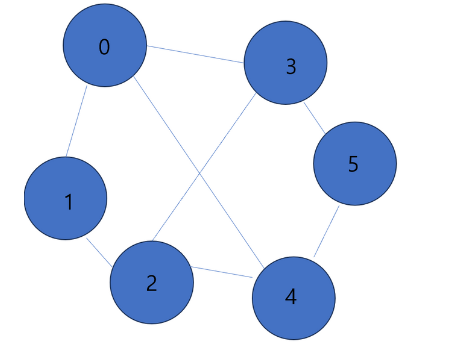
- 결국 stack이 비면서 DFS 연산이 끝난다.
- DFS는 깊이 우선 탐색이라고 위에서 말했다
- 위 연산을 보면 연관되어 있는 정점을 더 이상 방문할 정점이 없을 때까지 깊이 있게 탐색하는 걸 볼 수 있다.
BFS(Breadth First Search)
- 관련 있는 노드를 먼저 탐색한다. 그 후 다음 노드의 관련 있는 노드를 탐색한다.
- 너비 우선탐색
- 구현 방법
- 큐
구현 방법
- DFS처럼
- 우선 방문한 정점을 다시 방문하는 일이 없도록 visited 배열을 만들어 준다.
- 0은 아직 방문하지 않았다는 의미
- 시작 정점 하나부터 queue에 넣는다.
- 시작정점 visited 배열을 1로 수정한다.
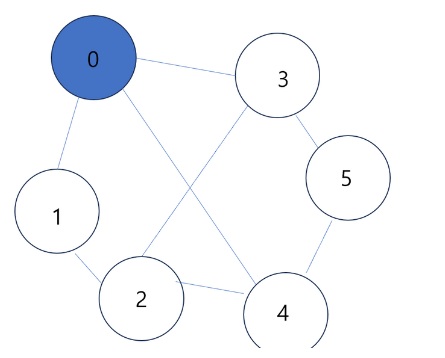
- <핵심로직>
- 큐를 deque 한다.
- deque 된 정점과 연결되고 방문한 적 없는 정점을 찾고 enque 한다.
- 연결되어 있는 visited 배열에 1로 수정한다.

- 위 핵심로직을 반복한다.
- 다음 deque 정점은 1이다.
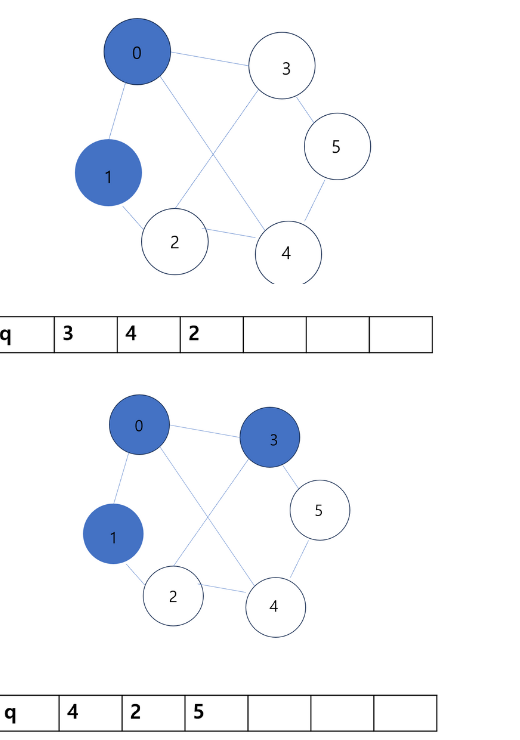
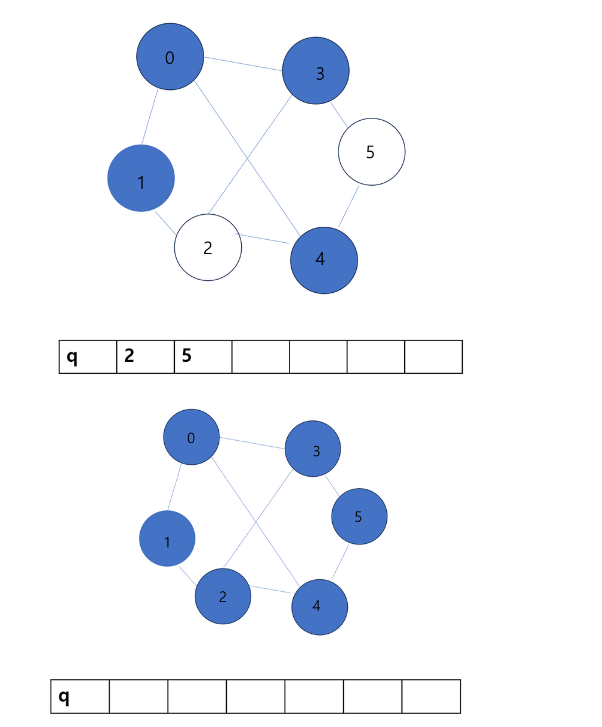
- queue의 원소가 비면 연산은 끝난다.
- 위 과정을 보면 왜 너비 우선 탐색과 다른지 알 수 있다.
수행시간
- 수행시간은 정점의 수가 K라면 O(K)로 DFS BFS 동일하다.
- 하지만 알고리즘 문제를 풀다 보면
- 문제마다 다르겠지만 BFS문제가 특정 정점을 찾는 문제에선 더 효율적이다.
구현 ( JAVA)
- DFS를 스택이 아닌 재귀함수로 구현함
package Main;
public class DFS_BFS {
// 시작 정점 정점수 ,visited 배열 , 인접행렬
public void DFS(int v, int N, int[] visited , int[][] adj_matrix) {
System.out.print("->"+v);
visited[v] = 1;
for (int i = 0; i < N; i++) {
if (adj_matrix[v][i] == 1 && visited[i] == 0) {
DFS(i, N, visited, adj_matrix);
}
}
}
public void BFS(int v, int N, int[] visited , int[][] adj_matrix) {
Queue<Integer> q = new Queue<Integer>();
q.enq(v);
visited[v] = 1;
while (!(q.isEmpty())) {
int temp = q.deq();
System.out.print("->" + temp);
for (int i = 0; i < N; i++) {
if (adj_matrix[temp][i] == 1 && visited[i] == 0) {
visited[i] = 1;
q.enq(i);
}
}
}
System.out.println();
}
}'cs > 알고리즘' 카테고리의 다른 글
| [알고리즘]Kruskal 알고리즘(java 구현) (0) | 2023.08.20 |
|---|---|
| [알고리즘] 이분 탐색이란(Binary Search) (0) | 2023.08.13 |
| [알고리즘] 브루트 포스 (완전 탐색)알고리즘이란 (0) | 2023.08.13 |
| [알고리즘] 분할 정복이란 (divide conquer) (0) | 2023.08.07 |
| [알고리즘] greedy 알고리즘 (탐욕 알고리즘) (0) | 2023.08.06 |




